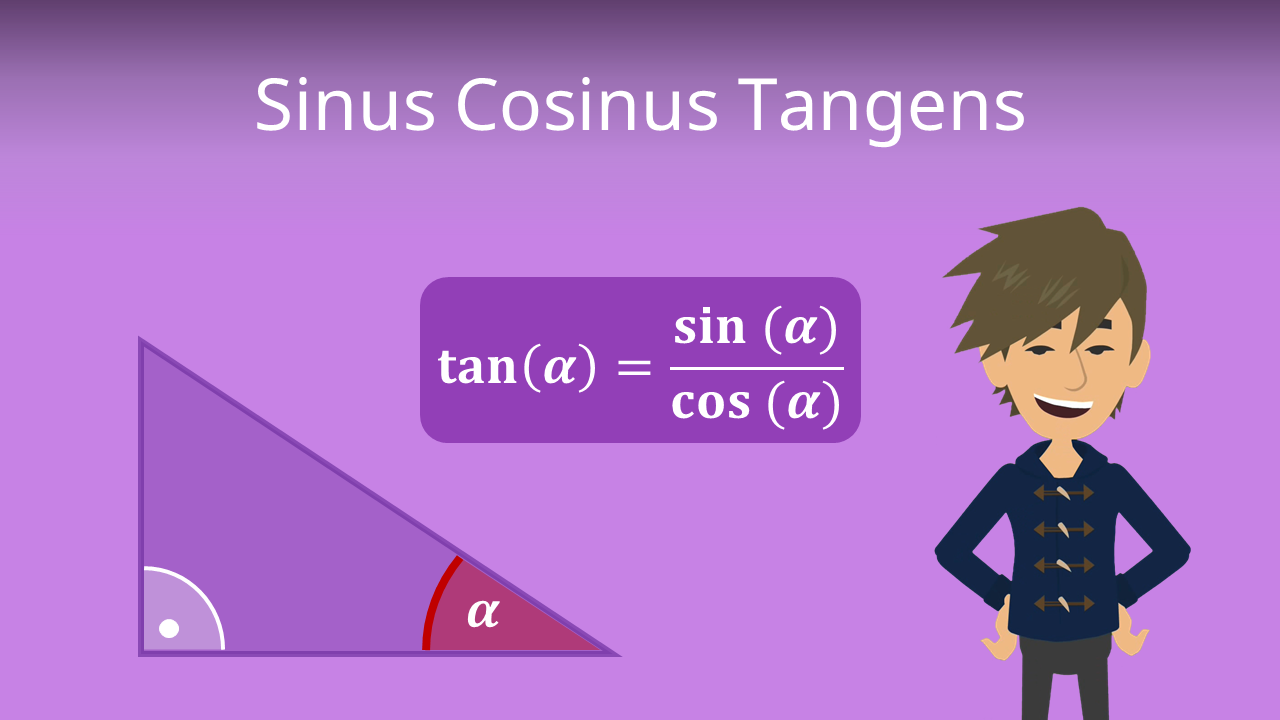
Der Sinus, der Cosinus und der Tangens werden angewendet, um Winkel und Seiten rechtwinkliger Dreiecke zu bestimmen.Mit dem Kosinus kannst du rechnen, wenn du zwei der drei Größen, Winkel, Ankathete und Hypotenuse gegeben hast und die dritte suchst. Das Vorgehen ist also ähnlich wie beim Sinus, nur mit der Ankathete anstatt der Gegenkathete eines Winkels.Der Vorteil des Kosinussatzes ist, dass die Werte immer eindeutig sind. Man erhält für die Winkelberechnung einen Wert von 0° bis 180° . Beim Sinussatz hingegen erhält man stets einen Winkel von 0° bis 90° und muss das Ergebnis rechnerisch bzw. mit der gegebenen Zeichnung überprüfen.

Wann wird der Sinus verwendet : Sinussatz. Den Sinussatz kannst du benutzen, um fehlende Stücke eines Dreiecks zu berechnen. Zum Beispiel, wenn zwei Seitenlängen und ein gegenüber liegender Winkel oder eine Seitenlänge und zwei Winkel gegeben sind. Das Dreieck muss dabei nicht rechtwinklig sein!
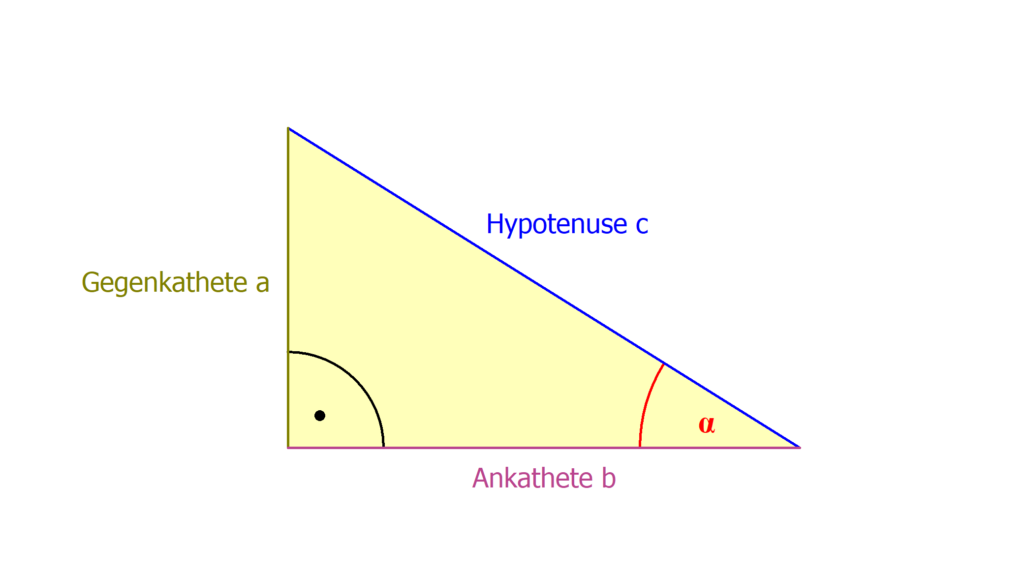
Woher weiß ich was Ankathete und Gegenkathete ist
Ankathete: Die Seite, die am Winkel. anliegt und nicht die Hypotenuse ist. Gegenkathete: Die Seite, die gegenüber vom Winkel. liegt und den Winkel nicht berührt.
Was ergibt sin * cos : Der Tangens als Quotient aus Sinus und Kosinus.
Kosinusfunktion – Symmetrie
Da du weißt, dass die Kosinusfunktion periodisch ist, kannst du eine weitere Eigenschaft erkennen: Die Kosinusfunktion ist achsensymmetrisch zur y-Achse. Zur Erinnerung: Eine Funktion ist achsensymmetrisch zur y-Achse, wenn gilt: f ( x ) = f ( – x ) .
Sinus- und Kosinusfunktion kurz und knapp
| Sinus | Kosinus | |
|---|---|---|
| y-Werte | -1 bis +1 | -1 bis +1 |
| Periodenlänge | 2 π bzw. 360° | 2 π bzw. 360° |
| Position der Hochpunkte | π2, 5π2, | 0, 2π, 4π, |
| Position der Tiefpunkte | 3π2, 7π2, | π, 3π, |
Was muss für den Sinussatz gegeben sein
Was besagt der Sinussatz
- müssen mindestens 3 Größen (Seitenlängen bzw. Winkel) bekannt sein und.
- unter den gegebenen Größen müssen eine Seitenlänge und der gegenüberliegende Winkel sein.
Die Winkelfunktionen Sinus, Kosinus und Tangens sind die wichtigsten trigonometrischen Funktionen. Sinus, Kosinus und Tangens beschreiben das Verhältnis von Seitenlängen in einem rechtwinkligen Dreieck in Abhängigkeit von einem der spitzen Winkel.In Jahrgangsstufe 10 erweitern die Schüler die Definition von Sinus und Kosinus auf beliebige Winkel; dabei werden neben geometrischen ausdrücklich auch funktionale Aspekte der Trigonometrie vom Lehrplan eingefordert.
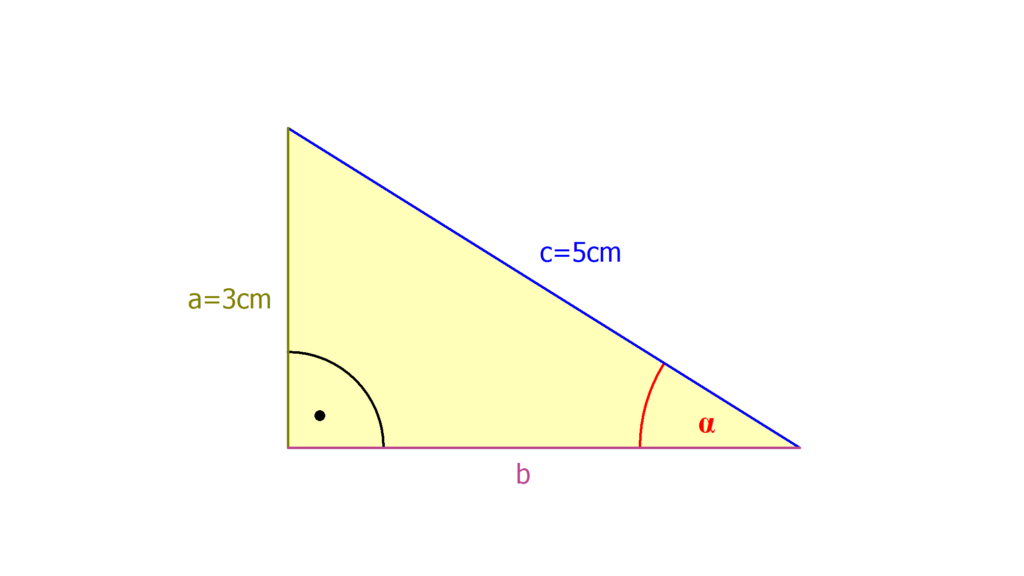
Nein, die Seite c ist nicht immer die Hypotenuse des Dreiecks. Welche Seite die Hypotenuse des rechtwinkligen Dreiecks ist, hängt von der Lage des rechten Winkels ab.
Für welche Winkel gilt sin : cos(360°-(α-180°))=-x und sin(360°-(α-180°))=y.
Wie findet man den Winkel heraus : Um einen Winkel α zu berechnen, bestimmst du das Verhältnis von Gegenkathete und Hypotenuse. Dafür teilst du die Gegenkathete durch die Hypotenuse (z.B. 3 : 6). Dein Ergebnis (hier: 0,5) setzt du in die Umkehrfunktion vom Sinus ein. Dann erhältst du den Winkel α = sin-1(0,5) = 30°.
Welche Periode hat Tangens
Die Tangensfunktion verläuft periodisch, das bedeutet, sie wiederholt sich in regelmäßigen Abständen. Die Länge der Periode beträgt 180° 180 ° 180° 180° oder π π π π im Bogenmaß. Das bedeutet, dass die Tangensfunktion sich alle 180° 180 ° 180° 180° wiederholt und dieselben Werte annimmt.

Daraufhin lernt man den Sinus als y-Koordinate eines Punktes auf dem Einheitskreis kennen, bei dem Winkel Werte zwischen 0° und 360° annehmen können und zum Teil schon in Radiant gemessen werden.Es gibt Dreiecke, die nicht mit dem Sinussatz berechnet werden können. Es gibt jedoch zwei Situationen, in den man den Sinussatz nicht anwenden kann. Zwei Seiten und ein Winkel sind bekannt, jedoch ist der bekannte Winkel eingeschlossen. Alle drei Seiten sind bekannt, jedoch kein Winkel!
In welchen Dreiecken gilt der Kosinussatz : Schon gewusst Der Kosinussatz wird manchmal auch als verallgemeinerter Satz des Pythagoras bezeichnet. Der Satz des Pythagoras gilt nämlich nur im rechtwinkligen Dreieck, also wenn γ = 90° ist. Dann ist cos(γ) = cos(90°) = 0.
