
Die Kettenregel besagt, dass die Verkettung von zwei differenzierbaren Abbildungen wieder differenzierbar ist. Ihre Ableitung erhält man, indem man die einzelnen Ableitungen verkettet.Häufig gestellte Fragen zum Thema Produktregel
Bei einer Funktion f(x) ist die Ableitungsfunktion f'(x) gleich dem Grenzwert des Differenzenquotienten für h strebend gegen null, also f'(x) = lim(h→0) [f(x+h) – f(x)] / h.Die Summenregel besagt, dass die Ableitung Funktion f(x)=g(x)+h(x) als Summe der beiden Funktionen g(x) und h(x) wie folgt lautet: f'(x)=g'(x)+h'(x).
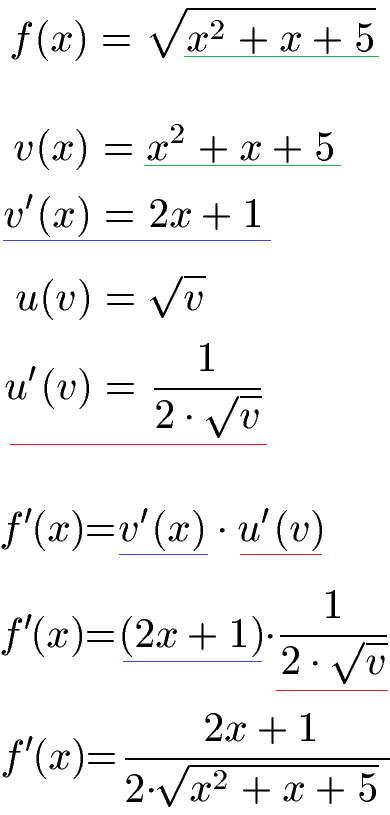
Wie leitet man Verkettungen ab : Bei der Ableitung von verketteten Funktion wird die Kettenregel verwendet: h ( x ) = f ( g ( x ) ) ⇒ h ′ ( x ) = f ′ ( g ( x ) ) ⋅ g ′ ( x ) .
Wann nutze ich die Kettenregel
Die Kettenregel wird angewandt, wenn zwei Funktionen ineinander verschachtelt, also verkettet sind. Ein Beispiel für eine verkettete Funktion ist: f(x) = (3x^2 – 1)^4. Es liegt eine innere Funktion vor 3x^2 – 1, auf die eine äußere Funktion (\blacksquare)^4 angewendet wird.
Was ist die lineare Kettenregel : Die Kettenregel besagt: Die Ableitung einer verketteten Funktion ist gleich dem Produkt der Ableitungen von äußerer und innerer Funktion an der jeweiligen Stelle. Für die Anwendung der Kettenregel ist eine auf der leibnizschen Schreibweise d y d x anstelle von f ' ( x ) beruhende Notation sehr einprägsam.
Die Produktregel ist bei ganzrationalen Funktionen am besten da anzuwenden, wenn das Ausmultiplizieren zu umständlich ist, wie z.B bei f ( x ) = x 2 ⋅ ( 2 x + 1 ) 3 . Um solch eine Funktion abzuleiten, benötigen Sie aber erst die Kettenregel, die auf den nächsten Seiten noch kommt.
Wie funktioniert die Kettenregel:
Sie wird benötigt, wenn beispielsweise eine an sich schon komplette Funktion von einer Klammer umschlossen wird, um die sich weitere Faktoren oder Polynome befinden. Dies sind zwei eigenständige Funktionen, welche bei einer Verkettung die oben stehende Funktion f(x) ergeben.
Für was braucht man die Quotientenregel
Wenn du einen Bruch ableiten musst und sowohl über als auch unter dem Bruchstrich ein x steht, dann brauchst du die Quotientenregel. Du benutzt die Ableitungsregel also, wenn du eine Funktion f(x) hast, die im Zähler g(x) und im Nenner h(x) ein x enthält.Die Produktregel ist bei ganzrationalen Funktionen am besten da anzuwenden, wenn das Ausmultiplizieren zu umständlich ist, wie z.B bei $f(x)=x^2\cdot (2x+1)^3$. Um solch eine Funktion abzuleiten, benötigen Sie aber erst die Kettenregel, die auf den nächsten Seiten noch kommt.Lineare Funktionen Formel: y = m x + b. Jede lineare Funktion kannst du mathematisch als Gerade oder als Gleichung darstellen. Die Gleichung nennst du dann die Funktionsgleichung. Das m ist die sogenannte Steigung und das b der y-Achsenabschnitt deiner linearen Funktion.

Regeln zur Teilbarkeit von Summen und Produkten
Ist eine natürliche Zahl Teiler zweier oder mehrerer Zahlen, so ist sie auch Teiler einer Summe oder Differenz aus diesen Zahlen. Ist in einem Produkt aus natürlichen Zahlen ein Faktor durch eine natürliche Zahl teilbar, so ist auch das Produkt durch diese Zahl teilbar.
Was ist die Ableitung von sin : Was ist die Ableitung des Sinus' Die Ableitung der Sinusfunktion f(x)=sin(x) ist f'(x)=cos(x).
Wann gilt Quotientenregel : Quotientenregel einfach erklärt
Du benötigst die Quotientenregel immer dann, wenn du einen Bruch von Funktionen ableiten willst. Das heißt, wenn im Zähler (oben) und im Nenner (unten) ein x vorkommt.
Wie kommt man auf die Quotientenregel
Quotientenregel – Merkregel
Bei der Quotientenregel rechnest du: NAZ minus ZAN durch Nenner im Quadrat. Im Zähler der Ableitung steht also Nenner mal Ableitung des Zählers minus Zähler mal Ableitung des Nenners. Anschließend teilst du noch durch das Quadrat des Nenners.

Um die Schnittpunkte der Graphen zweier Funktionen f und g zu bestimmen, setzt du die Funktionsterme gleich und löst die entstandene Gleichung nach x auf. Die Schnittpunkte haben die Koordinaten P(x0|f(x0))=P(x0|g(x0)).Wichtige Funktionstypen und ihre Eigenschaften
- Lineare Funktionen – Geraden.
- Quadratische Funktionen – Parabeln.
- Potenz- und Wurzelfunktionen.
- Polynomfunktionen beliebigen Grades.
- Gebrochen-rationale Funktionen.
- Exponential- und Logarithmusfunktion.
- Trigonometrische Funktionen.
Was ist die Summenregel Beispiel : Anwendung der Summenregel: Beispiel
Wir haben die Funktion f(x)= 6 \cdot x^4+2 \cdot x^3 gegeben. Die Summenregel besagt, dass wir die Summanden einzeln ableiten können. Wir haben also die Ableitung gebildet, indem wir die zwei Summanden separat abgeleitet haben (jeweils nach der Potenzregel).
