
Jeder Vektor hat einen Einheitsvektor, den du berechnen kannst. Davon gibt es nur eine Ausnahme: den Nullvektor →0=(00). Mit Einheitsvektoren kann man zum Beispiel die Richtung im zwei- oder dreidimensionalen Raum angeben, wenn die Länge keine Rolle spielt.Die Länge eines Vektors erhält man, indem man seine Koordinaten quadriert, summiert und dann die Wurzel zieht. Die Vorzeichen der Koordinaten spielen dabei keine Rolle.Der Einheitsvektor e → A B → zeigt in Richtung des Vektors A B → , ist jedoch auf die Länge normiert worden. Der Vektor A B → besitzt hingegen die Länge .

Wie berechnet man den Vektor : Um den Vektor zu berechnen, der die Punkte A und B verbindet, musst du A von B abziehen. Der Verbindungsvektor beginnt dann bei A (Fußpunkt) und endet bei B (Spitze). Auch im Dreidimensionalen kannst du einen Vektor aus zwei Punkten bestimmen.
Welche Vektoren haben die Länge 1
Einheitsvektoren (Vektoren mit der Länge 1) zeigen Dir die Richtung eines Vektors oder einer Koordinatenachse im Koordinatensystem an. Somit kannst Du mit Einheitsvektoren von einem Punkt im Koordinatensystem auch Strecken antragen.
Wie berechnet man den Einheitsvektor : Die Formel für die Berechnung des Einheitsvektors lautet: Den Einheitsvektor erhalten wir, indem wir den Vektor durch seine Länge teilen.
Merke. Ein Vektor ist eine physikalische Größe, die durch Angabe eines Zahlenwertes, ihrer Einheit und zusätzlich durch eine Richtung charakterisiert ist.
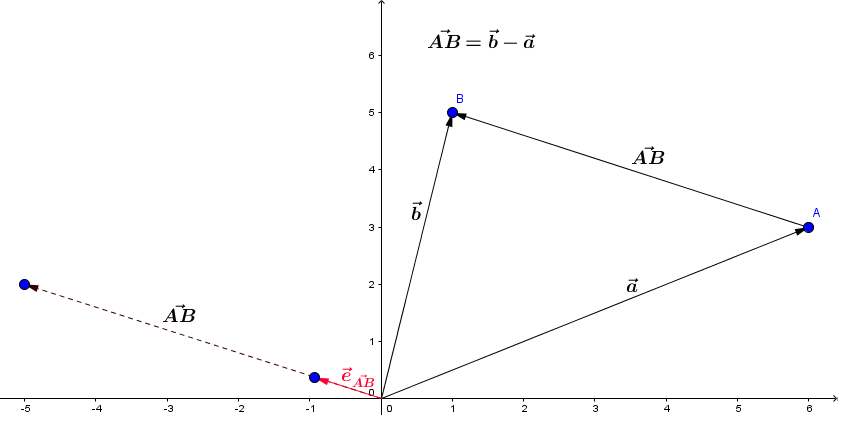
Einheitsvektoren (Vektoren mit der Länge 1) zeigen Dir die Richtung eines Vektors oder einer Koordinatenachse im Koordinatensystem an. Somit kannst Du mit Einheitsvektoren von einem Punkt im Koordinatensystem auch Strecken antragen.
Wie berechnet man Vektor V
Formel für den Betrag eines Vektors
- Die Formel zum Berechnen des Betrags für einen Vektor →v=(v1v2) im zweidimensionalen Raum lautet:
- |→v|=√v21+v22.
- Im dreidimensionalen Raum sieht das für den Vektor →v=(v1v2v3) so aus:
- |→v|=√v21+v22+v23.
Ein Normalenvektor →n ist dadurch definiert, dass er auf einer gegebenen Ebene, Fläche oder Gerade senkrecht steht. Wenn der Normalenvektor den Betrag 1 hat (normiert ist), nennt man ihn Normaleneinheitsvektor und schreibt →n0 oder ˆn.Ein Einheitsvektor ist in der analytischen Geometrie ein Vektor der Länge Eins. In der linearen Algebra und der Funktionalanalysis wird der Begriff der Länge auf allgemeine Vektorräume zum Begriff der Norm verallgemeinert.

Einheitsvektoren (Vektoren mit der Länge 1) zeigen Dir die Richtung eines Vektors oder einer Koordinatenachse im Koordinatensystem an. Somit kannst Du mit Einheitsvektoren von einem Punkt im Koordinatensystem auch Strecken antragen.
