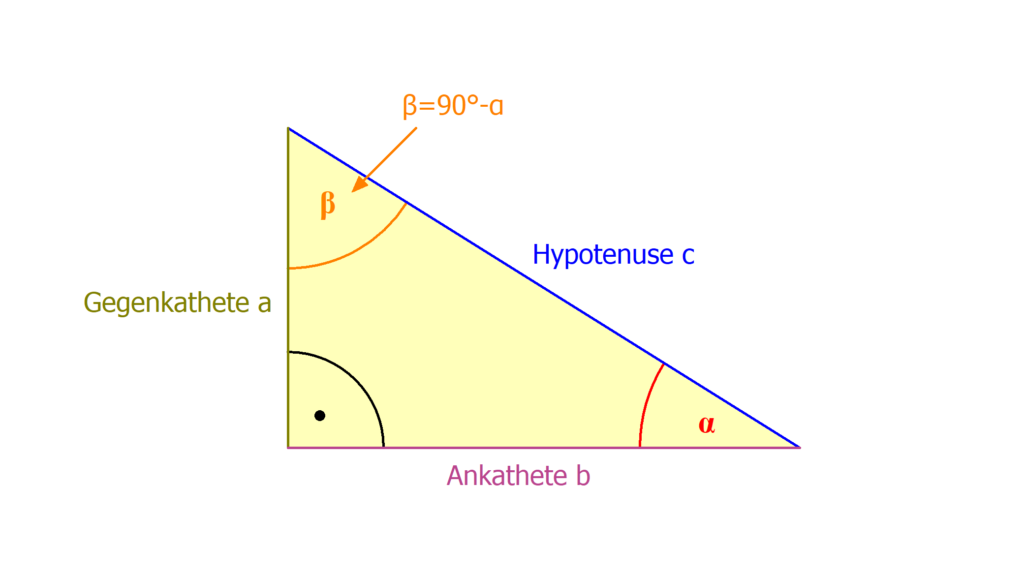
Als allgemeine Gleichung einer Kosinusfunktion wird oft f(x)=a · cos (bx + c) + d bezeichnet. Reelle Zahlen a, b, c und d haben folgende Effekte: a streckt entlang der y-Achse.Mit dem Sinus kann man entweder die Länge der Hypotenuse oder die Länge der Gegenkathete oder die Größe des Winkels berechnen, je nachdem, welche der drei Größen gesucht ist. Die jeweils anderen beiden Größen müssen gegeben sein.Definition des Kosinus
Er gibt das Verhältnis zwischen Winkel, Ankathete und Hypotenuse an. Der Kosinus wird mathematisch \cos(\alpha) abgekürzt.
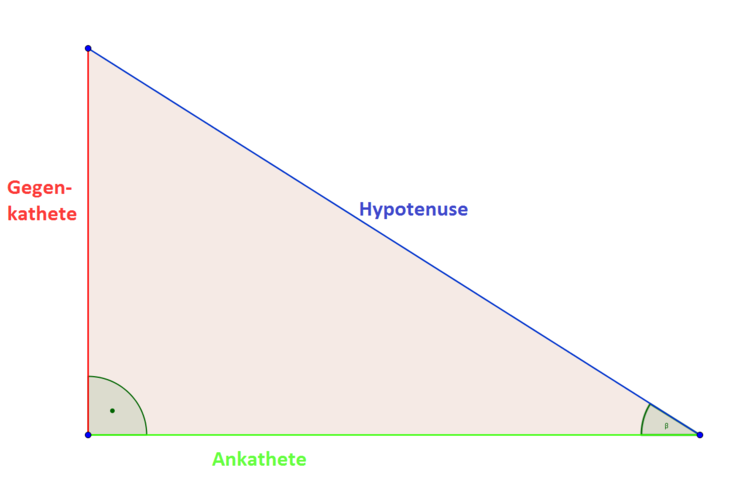
Wie berechne ich den Sinus mit dem Taschenrechner : Um den Sinuswert mit dem Taschenrechner zu berechnen, gibt man den Winkel in Grad ein (zum Beispiel 30°) und drückt die SIN-Taste; das Ergebnis für 30° ist 0,5.
Was ist der Cosinus von 90
Der genau Wert von cos(90°) cos ( 90 ° ) ist 0 .
Was ist der Cosinus von 60 : Daher ist cos 60°=0,5. Zu jedem Winkel gehört eine Länge des Kreisbogens.
sin cos tan Tabelle
| Winkel α im Gradmaß | sin(α) gerundet |
|---|---|
| 45° (-315°) | 0,7071 |
| 60° (-300°) | 0,8660 |
| 75° (-285°) | 0,9659 |
| 90° (-270°) | 1,0000 |
Nach der Definition ist der Sinus von 30 Grad gleich ½, und der Kosinus von 30 Grad ist √ 3/2.
Was ist der cos von 45
sin cos tan Tabelle
| Winkel α im Gradmaß | cos(α) gerundet |
|---|---|
| 30° (-330°) | 0,8660 |
| 45° (-315°) | 0,7071 |
| 60° (-300°) | 0,5000 |
| 75° (-285°) | 0,2588 |
Nach der Definition ist der Sinus von 30 Grad gleich ½, und der Kosinus von 30 Grad ist √ 3/2.Um einen Winkel α zu berechnen, bestimmst du das Verhältnis von Gegenkathete und Hypotenuse. Dafür teilst du die Gegenkathete durch die Hypotenuse (z.B. 3 : 6). Dein Ergebnis (hier: 0,5) setzt du in die Umkehrfunktion vom Sinus ein. Dann erhältst du den Winkel α = sin-1(0,5) = 30°.
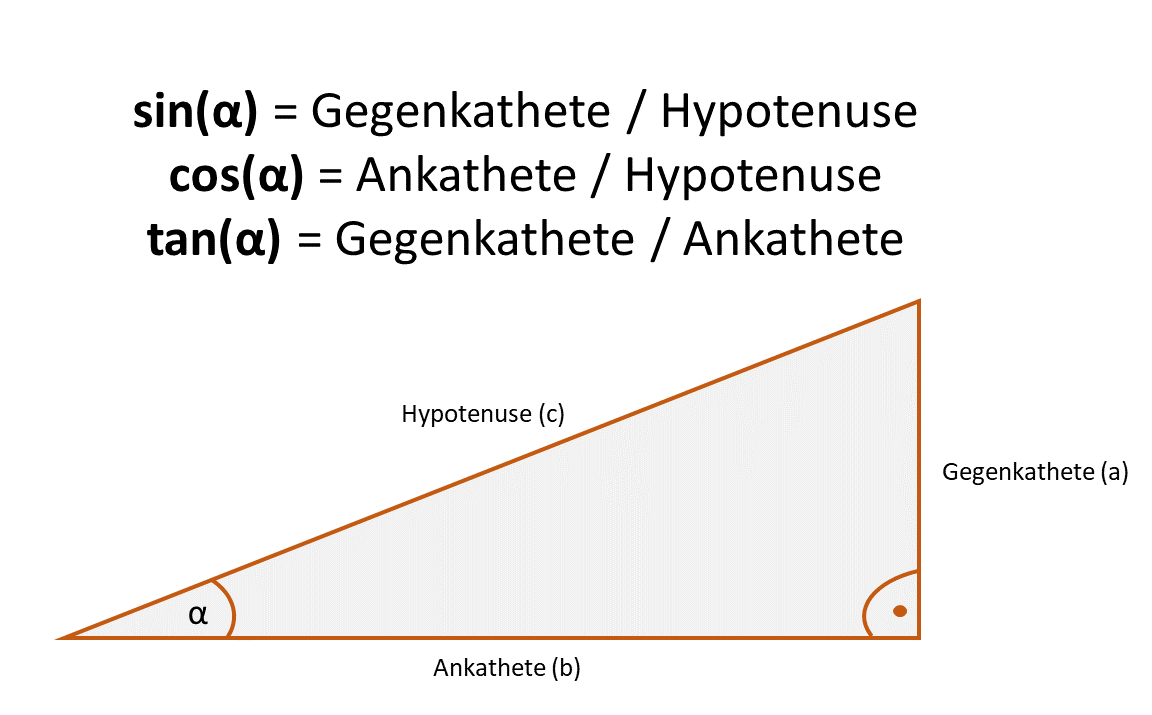
In den Aufgaben werden Buchstaben für die Hypotenuse (c), die Gegenkathete von α (a) und die Ankathete von α (b) verwendet. Dann sind die Formeln für die Winkelfunktionen: sin(α) = cos(β) = a/c. cos(α) = sin(β) = b/c.
Wie groß ist der Sinus von 45 Grad : sin cos tan Tabelle
| Winkel α im Gradmaß | sin(α) gerundet |
|---|---|
| 45° (-315°) | 0,7071 |
| 60° (-300°) | 0,8660 |
| 75° (-285°) | 0,9659 |
| 90° (-270°) | 1,0000 |
Wie viel ist der Sinus von 30 Grad : Nach der Definition ist der Sinus von 30 Grad gleich ½, und der Kosinus von 30 Grad ist √ 3/2.
Was ist der Sinus von 15
sin cos tan Tabelle
| Winkel α im Gradmaß | sin(α) gerundet |
|---|---|
| 15° (-345°) | 0,2588 |
| 30° (-330°) | 0,5000 |
| 45° (-315°) | 0,7071 |
| 60° (-300°) | 0,8660 |

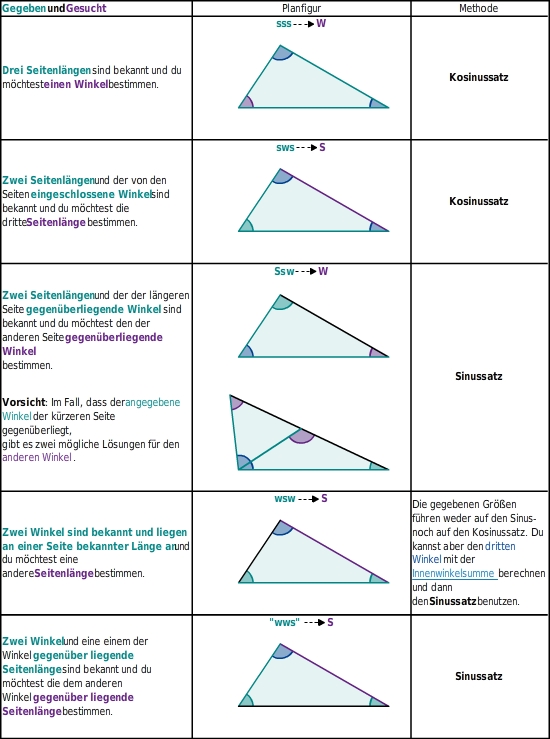
Der genau Wert von sin(60°) sin ( 60 ° ) ist √32 . Das Ergebnis kann in mehreren Formen wiedergegeben werden. Diese Website verwendet Cookies, um sicherzustellen, dass du das beste Erlebnis auf unserer Website erhältst.Mit dem Sinussatz kannst Du Seiten und Winkel in jedem Dreieck bestimmen, solange Du nur ein „Seiten-Winkel-Paar“ und eine weitere Größe kennst. An diesem Dreieck sind die drei Seiten und deren gegenüberliegenden Winkel dargestellt.
Wie bekomme ich den Winkel raus : Um einen Winkel α zu berechnen, bestimmst du das Verhältnis von Gegenkathete und Hypotenuse. Dafür teilst du die Gegenkathete durch die Hypotenuse (z.B. 3 : 6). Dein Ergebnis (hier: 0,5) setzt du in die Umkehrfunktion vom Sinus ein. Dann erhältst du den Winkel α = sin-1(0,5) = 30°.
