Eine hinreichende Bedingung für eine Wendestelle ist, dass die zweite Ableitung null wird und die dritte Ableitung an dieser Stelle ungleich null ist. Eine andere hinreichende (und oft leichter zu überprüfende) Bedingung hierfür ist, dass die zweite Ableitung verschwindet und an dieser Stelle ihr Vorzeichen wechselt.Um die Wendepunkte zu berechnen, muss man folgende Schritte ausführen:die zweite und die dritte Ableitung berechnen (f''(x) und f'''(x))die zweite Ableitung = Null setzen mit f''(x)=0 die Wendestelle xW berechnen (Gleichung nach x auflösen), d.h. den x-Wert des Wendepunktes berechnenmit f'''(xW) überprüfen, ob der …Das notwendige Kriterium für Wendepunkte lautet: Die 2. Ableitung muss 0 sein.

Was macht man mit der 3 Ableitung : Der Wechsel des Krümmungsverhaltens vom Graph einer Funktion an der Stelle x0 wird durch den Wert der 3. Ableitung der Funktion bestimmt.
Warum Wendepunkt zweite Ableitung Null
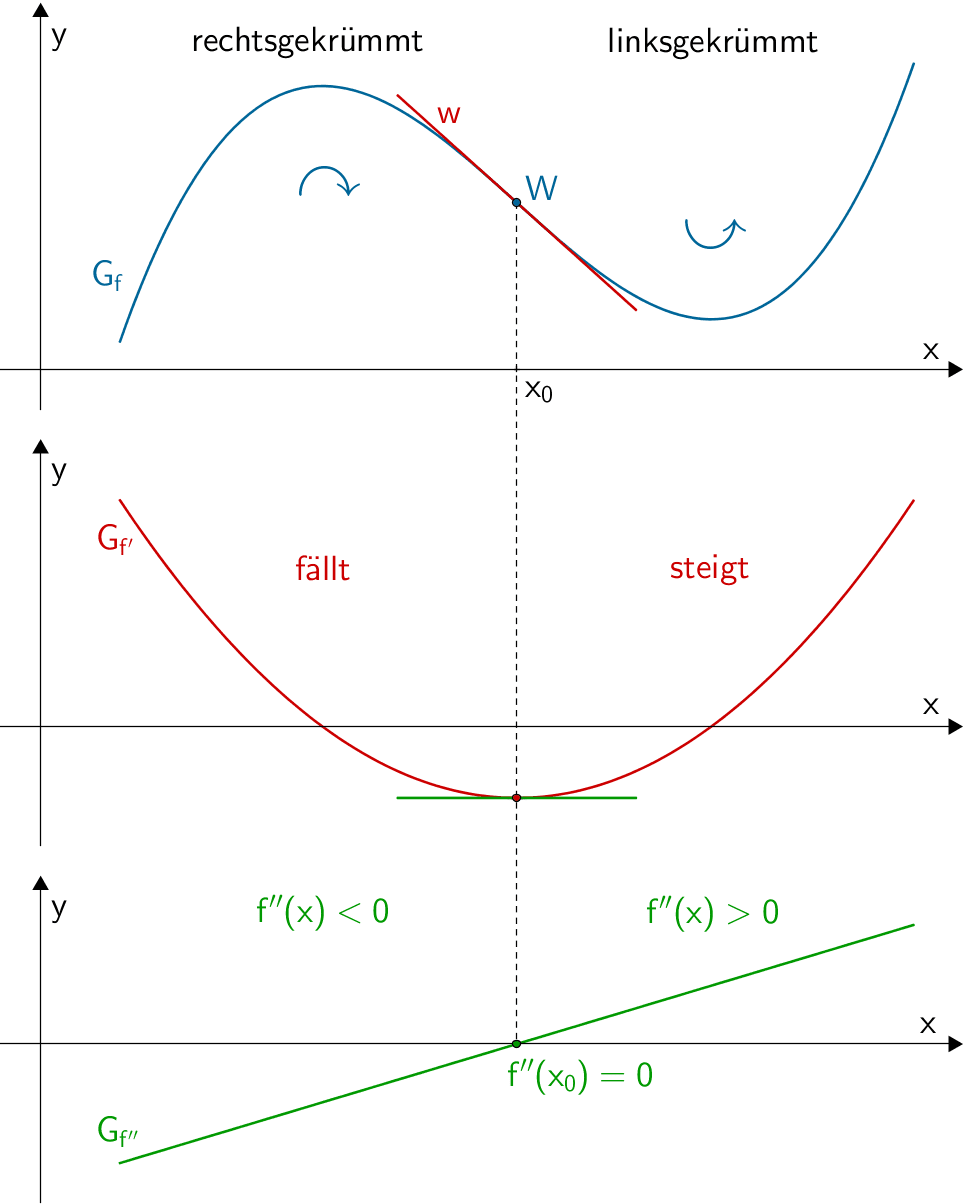
Wendepunkte – Graphische Bedeutung
Es wird deutlich: Die Nullstellen der ersten Ableitung sind die Stellen, an denen die Funktion ihre Extrema hat. Die Nullstelle der zweiten Ableitung ist die Stelle, an dem die erste Ableitung ein Extremum und die ursprüngliche Funktion einen Wendepunkt hat.
Welche Ableitung für Hochpunkt : Willst du testen, ob es sich um einen Hochpunkt oder Tiefpunkt handelt, brauchst du die zweite Ableitung f''(x). In die setzt du die Nullstelle xs der ersten Ableitung ein: Ist f''(xs) < 0, dann handelt es sich um einen Hochpunkt. Ist f''(xs) > 0, dann hast du einen Tiefpunkt.
Die zweite Ableitung hilft, das Krümmungsverhalten der Funktion f ( x ) f(x) f(x) zu untersuchen, denn sie gibt die Änderung der Steigung an. Mit der Berechnung von f ′ ′ ( x ) f^{\prime\prime}(x) f′′(x) kann bestimmt werden, ob es sich um eine Rechtskrümmung oder eine Linkskrümmung handelt.
Die erste Ableitung gibt für jede Funktion f(x) die Steigung (Anstieg) des Graphen an. Mit ihrer Hilfe kann man für jede Stelle x die Steigung des Graphen in dem Punkt berechnen. Man setzt also den x-Wert in die erste Ableitung ein und berechnet, wie groß der Anstieg der Funktion in dem entsprechenden Punkt ist.
Was ist ein Wendepunkt in der 2 Ableitung
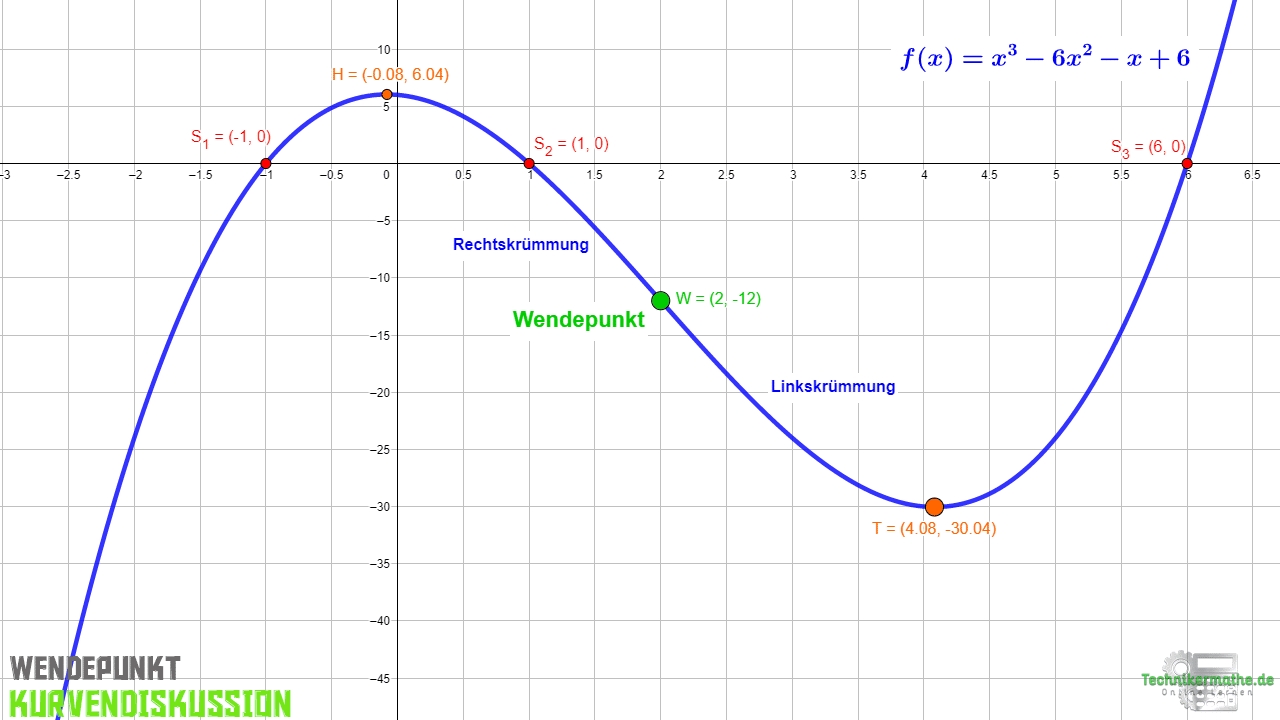
Erinnere dich: Ein Wendepunkt zeigt an, dass die Kurve ihr Krümmungsverhalten ändert, also sich von rechts nach links krümmt oder umgekehrt. Du weißt außerdem, dass du anhand der zweiten Ableitung das Krümmungsverhalten ablesen kannst.Die zweite Ableitung hilft, das Krümmungsverhalten der Funktion f ( x ) f(x) f(x) zu untersuchen, denn sie gibt die Änderung der Steigung an. Mit der Berechnung von f ′ ′ ( x ) f^{\prime\prime}(x) f′′(x) kann bestimmt werden, ob es sich um eine Rechtskrümmung oder eine Linkskrümmung handelt.Du weißt bereits, dass es eine hinreichende Bedingung für einen Wendepunkt ist, wenn die dritte Ableitung ungleich Null ist. Was passiert aber, wenn die dritte Ableitung gleich Null sein sollte Dann hilft dir diese Aussage leider nicht weiter. Es könnte sich dennoch um einen Wendepunkt handeln – oder auch nicht.
Um zu bestimmen, ob es ein links-rechts, oder rechts-links Wendepunkt ist, bestimmt ihr die 3. Ableitung und guckt, ob diese positiv oder negativ ist: f´´´(x)=6. → Es ist ein rechts-links Wendepunkt.
Für was benötigt man die 2 Ableitung : Die zweite Ableitung hilft, das Krümmungsverhalten der Funktion f ( x ) f(x) f(x) zu untersuchen, denn sie gibt die Änderung der Steigung an. Mit der Berechnung von f ′ ′ ( x ) f^{\prime\prime}(x) f′′(x) kann bestimmt werden, ob es sich um eine Rechtskrümmung oder eine Linkskrümmung handelt.
Welche Ableitung für hoch und Tiefpunkt : Willst du testen, ob es sich um einen Hochpunkt oder Tiefpunkt handelt, brauchst du die zweite Ableitung f''(x). In die setzt du die Nullstelle xs der ersten Ableitung ein: Ist f''(xs) < 0, dann handelt es sich um einen Hochpunkt. Ist f''(xs) > 0, dann hast du einen Tiefpunkt.
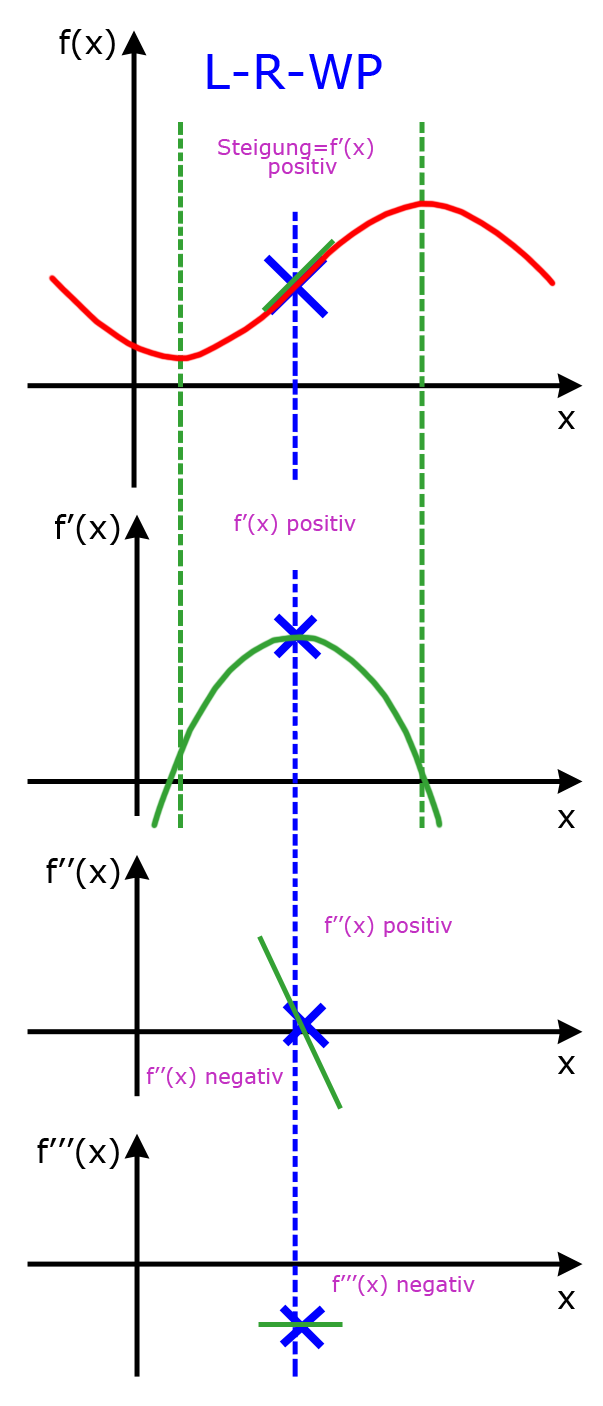
Wann links rechts Wendepunkt
Beim Wendepunkt berechnen müssen zwei Bedingungen erfüllt sein: f“(x) = 0 und f“'(x) ≠ 0. Ist die dritte Ableitung f“'(x) > 0, handelt es sich um einen Rechts-links-Wendepunkt. Ist die dritte Ableitung f“'(x) < 0, handelt es sich um einen Links-rechts-Wendepunkt.
Die zweite Ableitung hilft zu entscheiden, ob sich eine Kurve im Uhrzeigersinn oder im Gegenuhrzeigersinn dreht, wenn wir uns im Koordinatensystem von links nach rechts bewegen. Die blaue Kurve dreht sich im Uhrzeigersinn. Man sagt auch, dass sie konkav ist.Dies entspricht der Steigung der Tangente und damit der Steigung des Graphen in dem gewählten Punkt. Geometrisch betrachtet gibt die erste Ableitung also die Steigung des Graphen an. Die zweite Ableitung ist ein Maß für die Krümmung eines Graphen in jedem seiner Punkte.
Was sagt uns die zweite Ableitung : Die zweite Ableitung hilft, das Krümmungsverhalten der Funktion f ( x ) f(x) f(x) zu untersuchen, denn sie gibt die Änderung der Steigung an. Mit der Berechnung von f ′ ′ ( x ) f^{\prime\prime}(x) f′′(x) kann bestimmt werden, ob es sich um eine Rechtskrümmung oder eine Linkskrümmung handelt.