
Das Integral ist ein Oberbegriff für das bestimmtes und unbestimmtes Integral. Ein bestimmtes Integral liefert einen Zahlenwert, während ein unbestimmtes Integral eine Funktion liefert. Die Integralrechnung steht in engem Zusammenhang mit der Differentialrechnung.Mithilfe eines Integrals lässt sich der Flächeninhalt zwischen einem Graphen und der x-Achse berechnen. Man unterscheidet allgemein zwischen einem unbestimmten und bestimmten Integral. Die untere Grenze eines bestimmten Integrals ist eine Nullstelle der Funktion.Die Integralrechnung ist nützlicher als man auf den ersten Blick denkt. Sie ist netter Begleiter bei der Kostenrechnung, bei Weg-Beschleunigungs- und Intervallfragen, und bei der Berechnung von elektrischen und magnetischen Feldern. Unverzichtbar ist sie allerdings bei der Bestimmung von Flächeninhalten und Volumina.

Wie rechnet man das Integral aus : Den Wert eines bestimmten Integrals über eine Funktion f berechnet man, indem man ihre Stammfunktion an den beiden Integrationsgrenzen auswertet und die Differenz der beiden bildet ("obere Grenze minus untere Grenze"). Die Konstante C, die in der allgemeinen Stammfunktion steht, fällt hierbei weg (hebt sich auf).
Was ist ein Beispiel für ein Integral
Wie bereits erwähnt gibt es bei der Integralrechnung auch eine Summenregel, die besagt, dass jeder Summand einzeln integriert wird. Zum Beispiel ist F ( x ) = x 2 + 3 x eine Stammfunktion von f ( x ) = 2 x + 3 .
Was ist das Integral von 0 : Der Wert des bestimmten Integrals wird 0, wenn die eingeschlossenen Flächeninhalte über und unter der x-Achse genau gleich groß sind.
Inhalte und Kompetenzen
| Kursphase (Klasse 12/13) | ||
|---|---|---|
| Grundkurs | Leistungskurs | |
| 1. Semester ma-1 | Differenzialrechnung | Differenzialrechnung |
| 2. Semester ma-2 | Integralrechnung & Stochastik | Integralrechnung & Stochastik |
| 3. Semester ma-3 | Analytische Geometrie | Analytische Geometrie |

Stammfunktion – Definition. Eine Stammfunktion ist vereinfacht gesagt eine differenzierbare Funktion, die abgeleitet immer die gleiche Funktion als Ergebnis hervorbringt. Dieser Prozess wird in der Mathematik als Integrieren bezeichnet. Die Funktion F(x) ist eine Stammfunktion von f(x), wenn gilt: F'(x)=f(x).
Ist das Integral positiv oder negativ
Flächen oberhalb der x-Achse sind positiv, Flächen unterhalb der x-Achse sind negativ. Orientierte Fläche bedeutet: Liegt die Fläche oberhalb der x-Achse, so ist das bestimmte Integral positiv. Liegt die Fläche unterhalb der x-Achse so ist das bestimmet Integral negativ.Die Integralfunktion wird mithilfe eines bestimmten Integrals angegeben. Eine Stammfunktion F ( x ) F(x) F(x) ist eine Funktion, die abgeleitet wieder f ( x ) f(x) f(x) ergibt. Dabei gibt es zu einer Funktion f ( x ) f(x) f(x) immer mehrere Stammfunktionen, da additive Konstanten beim Ableiten wegfallen.Alle Themenbereiche in Mathematik, 13. Klasse
- Geometrie.
- Lineare Algebra und Analytische Geometrie.
- Wahrscheinlichkeitsrechnung und Stochastik.
- Zahlen, Rechnen und Größen.
- Funktionen.
- Terme und Gleichungen.
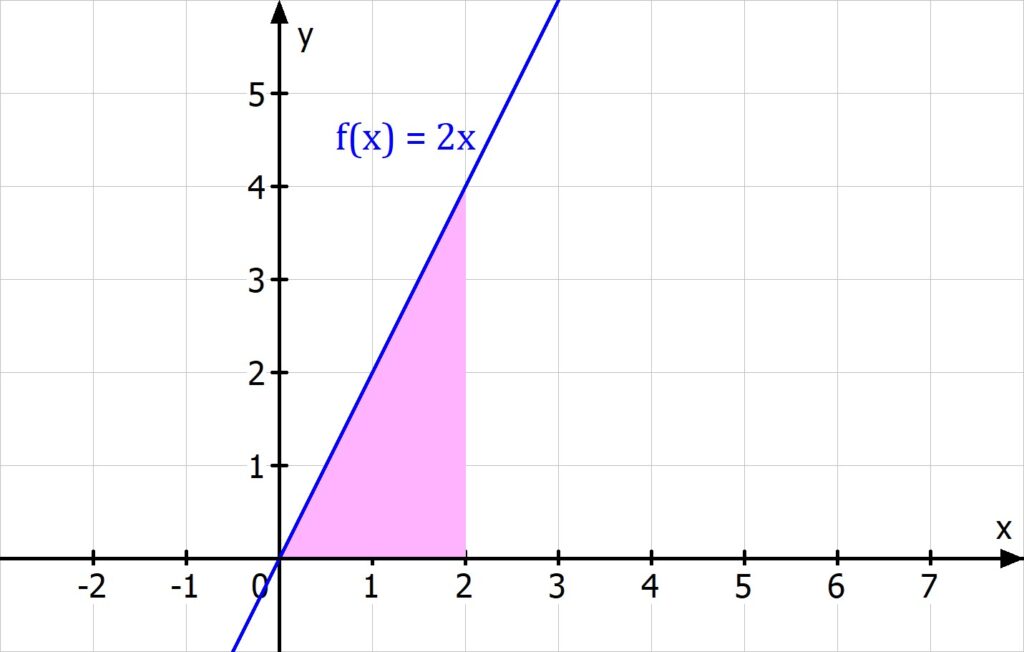
In der Integralrechnung unterscheidest du zwischen dem unbestimmten und dem bestimmten Integral. Das unbestimmte Integral gibt die Menge aller Stammfunktionen einer Funktion f(x) an. Das bestimmte Integral verwendest du, um den Flächeninhalt unter einem Funktionsgraphen zu bestimmen.
Was ist eine Stammfunktion Beispiel : Anwendung Potenzregel — Potenzfunktionen
In beiden Fällen erhältst du wieder f(x) = x2, wenn du nach x ableitest. Eine konkrete Stammfunktion zu f(x) = 1 wäre somit beispielsweise F(x)= x+4 (c = 4) oder F(x)= x (c = 0).
Woher weiß ich ob ein Integral positiv oder negativ ist : Liegt die Fläche oberhalb der x-Achse, so ist das bestimmte Integral positiv. Liegt die Fläche unterhalb der x-Achse so ist das bestimmet Integral negativ.
Hat eine Integralfunktion immer eine Nullstelle
Jede Integralfunktion ist eine Stammfunktion. Graphen von f und der x-Achse im Intervall [u ; x]. Jede Integralfunktion hat an der Stelle x = u eine Nullstelle.
Du wirst in diesem Schuljahr lernen, wie Lineare Gleichungssysteme mit zwei Variablen funktionieren und wie du sie mit dem Gleichsetzungsverfahren, dem Einsetzungsverfahren oder dem Additionsverfahren lösen kannst. Außerdem lernst du lineare Ungleichungen und Bruchgleichungen kennen.Gesamtschule (Klasse 5–12/13)
Was genau ist die Stammfunktion : Eine Stammfunktion oder ein unbestimmtes Integral ist eine mathematische Funktion, die man in der Differentialrechnung, einem Teilgebiet der Analysis, untersucht. Es kann je nach Kontext erforderlich sein, zwischen diesen beiden Begriffen zu unterscheiden.
