
Die zweite binomische Formel erhältst du, indem du das Produkt ( a − b ) 2 = ( a − b ) ⋅ ( a − b ) (a-b)^2 = (a-b) \cdot (a-b) (a−b)2=(a−b)⋅(a−b) ausmultiplizierst und gleichartige Terme zusammenfasst.Die drei Binomischen Formeln (BF) lauten: (a + b)² = a² + 2ab + b² (a − b)² = a² − 2ab + b² (a + b) (a − b) = a² − b²1. binomische Formel: (a+b)2=a2+2ab+b2. 2. binomische Formel: (a−b)2=a2−2ab+b2.
Wie löst man die binomische Formel auf : Besteht ein Term in der binomischen Formel aus einem Produkt aus zwei (oder mehreren) Faktoren, löst du ZUERST die binomische Formel auf indem du die Faktoren als untrennbare Einheit behandelst. DANACH kannst du das Ergebnis vereinfachen, indem du alle Zahlenwerte multiplizierst.
Was sagt die binomische Formel aus
Es gibt drei binomische Formeln. Diese sind ein wichtiges Hilfsmittel zur Vereinfachung von Termen und können in beiden Richtungen angewendet werden. Das bedeutet, dass sie sowohl zum Ausklammern, als auch zum Faktorisieren verwendet werden können.
Was ergibt A A : A + A = A oder 0. A + B = A oder B oder 0 oder AB. A + AB = A oder B oder AB. B + B = B oder 0.
Es gibt drei binomische Formeln. Diese sind ein wichtiges Hilfsmittel zur Vereinfachung von Termen und können in beiden Richtungen angewendet werden. Das bedeutet, dass sie sowohl zum Ausklammern, als auch zum Faktorisieren verwendet werden können.
Es gibt drei binomische Formeln:
- binomische Formel: ( a + b ) 2 = a 2 + 2 a b + b 2 ~(a+b)^2 =a^2+2ab+b^2 (a+b)2=a2+2ab+b2.
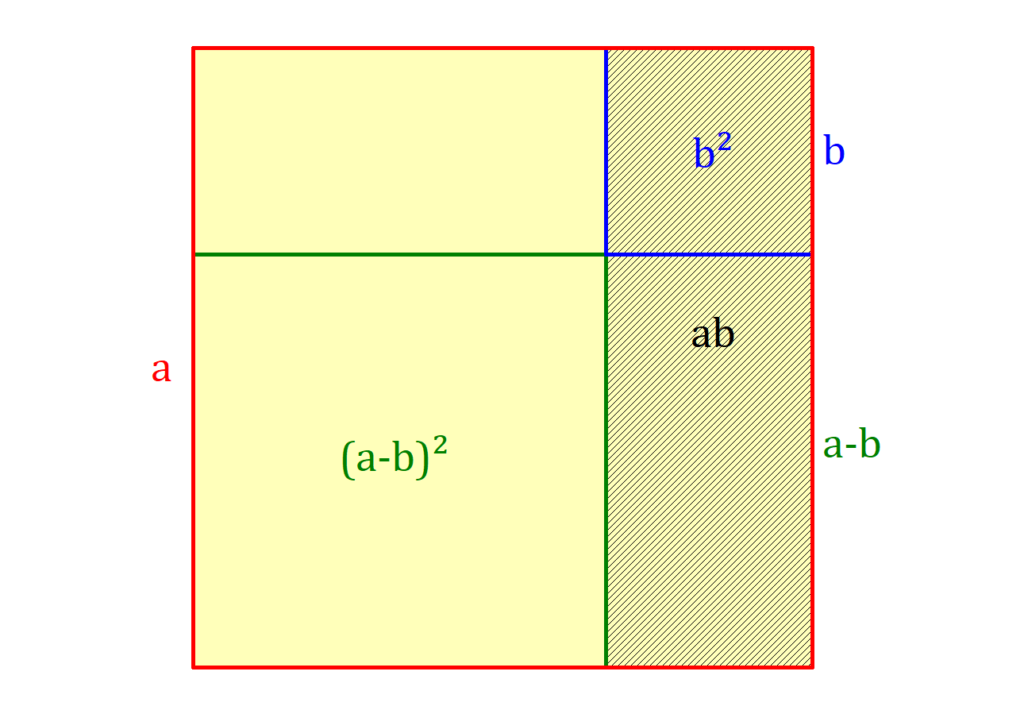
- binomische Formel: ( a − b ) 2 = a 2 − 2 a b + b 2 ~(a-b)^2 =a^2-2ab+b^2 (a−b)2=a2−2ab+b2.
- binomische Formel: ( a + b ) ⋅ ( a − b ) = a 2 − b 2 ~(a+b)\cdot (a-b) =a^2-b^2 (a+b)⋅(a−b)=a2−b2.
Wann benutze ich die 3 binomische Formel
Wenn du also zwei Zahlen oder Buchstaben in der Klammer hast und auch noch eine 2 im Exponent, brauchst du die drei binomischen Formeln. Mit den binomischen Formeln kannst du dabei die Klammern auflösen.Ein Binom ist ein Polynom aus nur zwei Gliedern (lateinisch „bi-“: zwei-), also einfach eine Summe oder Differenz aus zwei Termen: 1 + 1; a + b; x – y; 5ax + 13z2. Große Bedeutung haben die binomischen Formeln für quadrierte Binome.Dafür gibt es eine andere abkürzende Schreibweise, nämlich die oben rechts am Buchstaben vermerkte Anzahl gleicher Faktoren in einem Produkt: a·a·a = a³. Die hochgestellte 3 nennt man auch Hochzahl oder Exponent.

Eine arithmetische Division durch null ist nicht möglich.
Was ist ein Binom Beispiel : Ein Binom ist ein Polynom aus nur zwei Gliedern (lateinisch „bi-“: zwei-), also einfach eine Summe oder Differenz aus zwei Termen: 1 + 1; a + b; x – y; 5ax + 13z2.
Was ist das 3 Binom : Die dritte binomische Formel brauchst du, wenn du zwei Binome miteinander multiplizieren willst: (a + b) · (a – b) = a2 – ab + ab – b2 = a2 – b2 .
Wie bildet man ein Binom
Oftmals trifft man im Mathematik Unterricht dabei auf den Exponenten 2: Die binomischen Formeln: Binomische Formel: (a + b)2 = a2 + 2ab + b. Binomische Formel: (a – b)2 = a2 – 2ab + b.

Das Ungleichheitszeichen ( ≠ ) ist ein durchgestrichenes Gleichheitszeichen und wird eingesetzt, wenn die Ungleichheit zweier Zahlen dargestellt werden soll. Das Identisch-Zeichen ( ≡ ) ist eine Form mit drei waagerechten Strichen und wird eingesetzt, wenn zwei arithmetische Ausdrücke identisch sind.Die Beziehung ist enthalten wird durch das Zeichen ⊆ symbolisiert. Beispiel: Die Menge {a, c, e} ist in der Menge {a, b, c, d, e} enthalten.
Was ist 7 geteilt durch 0 : das Teilen durch Null hat keine Bedeutung.
