Der Umfang ist die Länge des Randes einer Figur. Du kannst den Umfang berechnen, indem du die Länge aller Seiten einer Figur miteinander addierst.Unter dem Umfang versteht man zunächst einmal die Strecke entlang einer Fläche. Anschaulich kann man sich das als die Länge einer Schnur vorstellen, die man genau einmal direkt an einer Fläche außen herum spannen kann. Je nach Figur sind hierbei verschiedene Vorgehensweisen nötig, um den Umfang zu bestimmen.Wie du gesehen hast, berechnest du den Umfang einer Figur, indem du ihre Seitenlängen miteinander addierst. Allgemein werden bei der Berechnung des Umfangs alle Seitenlängen addiert. Je nach Figur variiert die Anzahl der Seiten und wie viele gleichlange Seiten es gibt.
Was ist mit Umfang gemeint : Mit dem Umfang meinen wir die Länge aller Seiten einer geometrischen Figur.
Was ist ein Umfang 4 Klasse
Der Umfang ist die Länge der Linie, die eine Figur begrenzt. Erste Übungen werden durch Umlegen gemacht.
Was ist ein Umfang Beispiel : Im Beispiel mit den Grundstücken ist der Umfang des Grundstücks die Länge des benötigten Zauns. Die Länge der Umrandung einer Fläche nennt man Umfang. Der Umfang ist die Summe aller Seitenlängen.
Der Durchmesser d ist die Länge der Verbindungsstrecke zweier Punkte der Kreislinie, die durch den Kreismittelpunkt verläuft. Der Umfang u ist die Länge der Kreislinie. Der Flächeninhalt A ist die Fläche, die von der Kreislinie begrenzt wird.
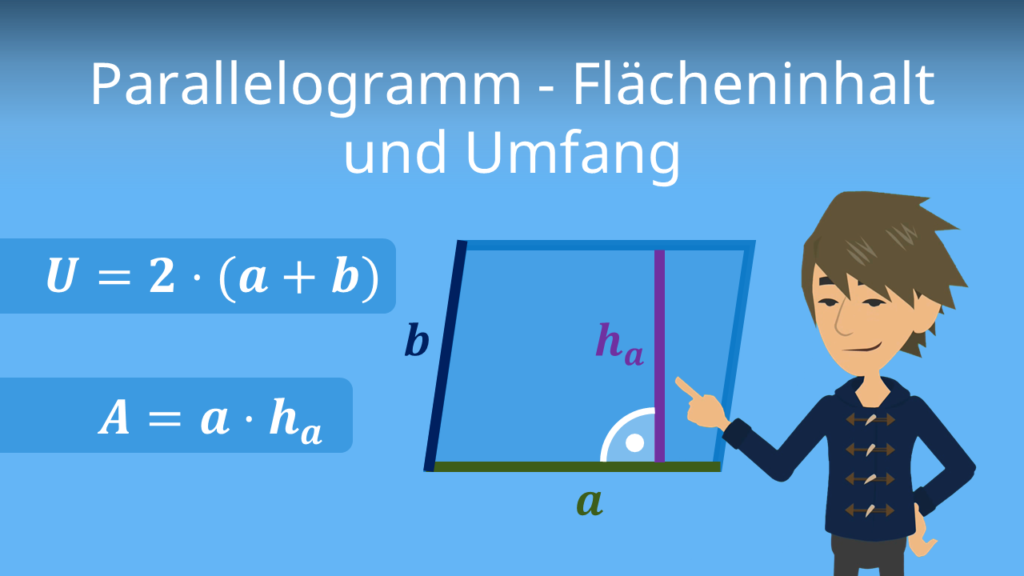
Der Umfang U einer Figur ist die Länge des Randes der Figur. Wir können den Umfang einer Figur herausfinden, indem wir die Längen aller Seiten der Figur addieren.
Wie misst man den Umfang von etwas
Den Umfang kannst du messen, indem du einen Faden um den Gegenstand legst und dann die Länge des Fadens misst. Berechne dann noch jeweils das Verhältnis von Umfang und Durchmesser, also ud. Bereits in der Bibel gibt es Hinweise darauf, dass die Menschen das Verhältnis von Umfang und Radius untersucht haben.Dem Umfang eines Quadrats berechnest du, indem du u = a+a+a+a rechnest, sodass du das Viereck einmal “umrundest”. Diese Formel für die Berechnung des Umfangs kann vereinfacht werden: u = 4*a.Flächeninhalt und Umfang
Mit dem Flächeninhalt misst du die Größe der Fläche einer Figur, zum Beispiel eines Rechtecks. Beim Umfang dagegen rechnest du alle Seiten der Figur zusammen (Summe der Seitenlängen). Er ist also die Länge der Linie um die Figur herum (Begrenzungslinie).

Der Umfang U ist die Länge der Kreislinie. Den Kreis Umfang berechnest du mit der Formel U = 2 · r · π oder U = d · π. Um den Kreis Umfang zu berechnen, brauchst du den Radius r oder den Durchmesser d. Der Radius r ist der Abstand von einem Punkt auf der Kreislinie zum Mittelpunkt M.
Welchen Umfang hat ein Kreis mit 5 cm Durchmesser : Benutze die entsprechende Gleichung, in diesem Fall ist die Formel für das Verhältnis von Umfang zu Durchmesser: U = πd. Setze den Durchmesser in die Gleichung ein: U = π ∙ (5 cm) = 15,708 cm .
Wie berechne ich Umfang Wenn ich Durchmesser habe : Den Kreisumfang (u) berechnst du, indem du den Durchmesser (d) mit der Kreiszahl Pi multiplizierst. Der Durchmesser ist nichts anderes, als zwei mal der Radius. Deshalb kannst du d auch durch 2 · r ersetzen. Noch ein Hinweis: Häufig rechnet man mit dem Näherungswert 3,14 für die Kreiszahl Pi.
Wie berechnet man den Umfang 5 Klasse
Dem Umfang eines Quadrats berechnest du, indem du u = a+a+a+a rechnest, sodass du das Viereck einmal “umrundest”. Diese Formel für die Berechnung des Umfangs kann vereinfacht werden: u = 4*a.
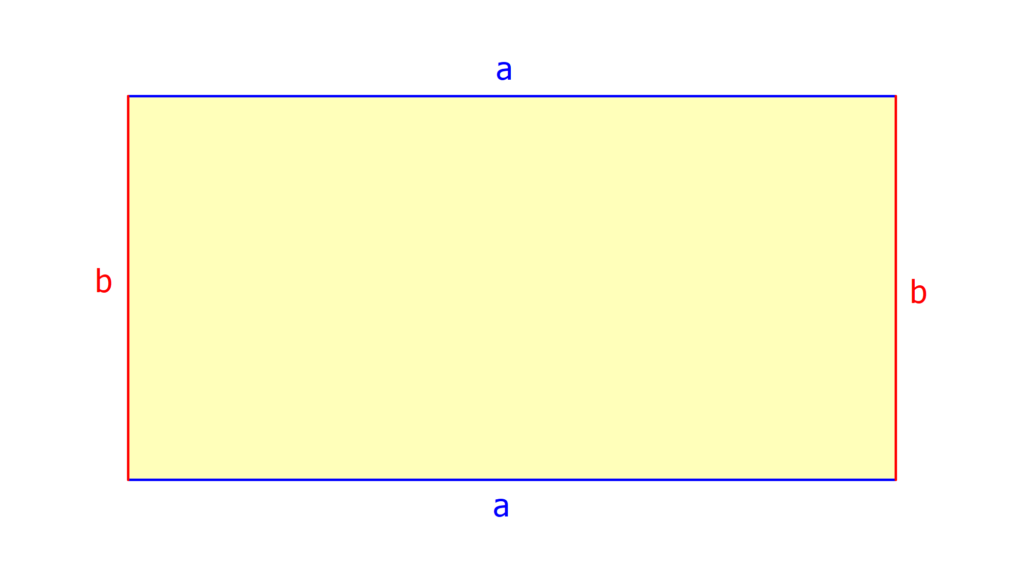
Du zählst zweimal die Länge a und zweimal die Breite b zusammen. Um den Rechteck Umfang zu berechnen, addierst du die Längen aller Seiten miteinander. Die Umfang Formel ist also U = 2 · a + 2 · b.Um den Umfang einer Figur zu berechnen, musst du alle Seiten der Figur addieren. In einem Rechteck sind die gegenüberliegenden Seiten gleich lang. In einem Quadrat sind alle Seiten gleich lang.
Wie berechne ich den Umfang einer Figur : Wie geht man vor um den Umfang einer zusammengesetzten Fläche zu berechnen Man startet an einem markierten Punkt und geht einmal um die Fläche rum. Dabei multipliziert man alle Längen und erhält den Umfang. Dabei addiert man alle Längen zusammen und erhält den Umfang.