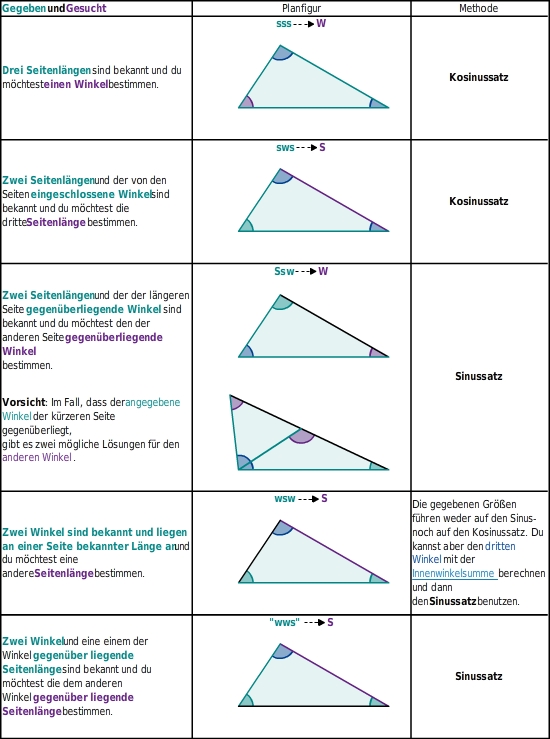
Der Sinussatz gibt eine Beziehung zwischen den Winkeln eines allgemeinen Dreiecks und den gegenüberliegenden Seiten an. Das bedeutet: Wenn du in einem allgemeinen Dreieck von je zwei Winkeln und den entsprechend gegenüberliegenden Seiten drei Größen kennst, kannst die fehlende vierte Größe berechnen.Definition des Sinus
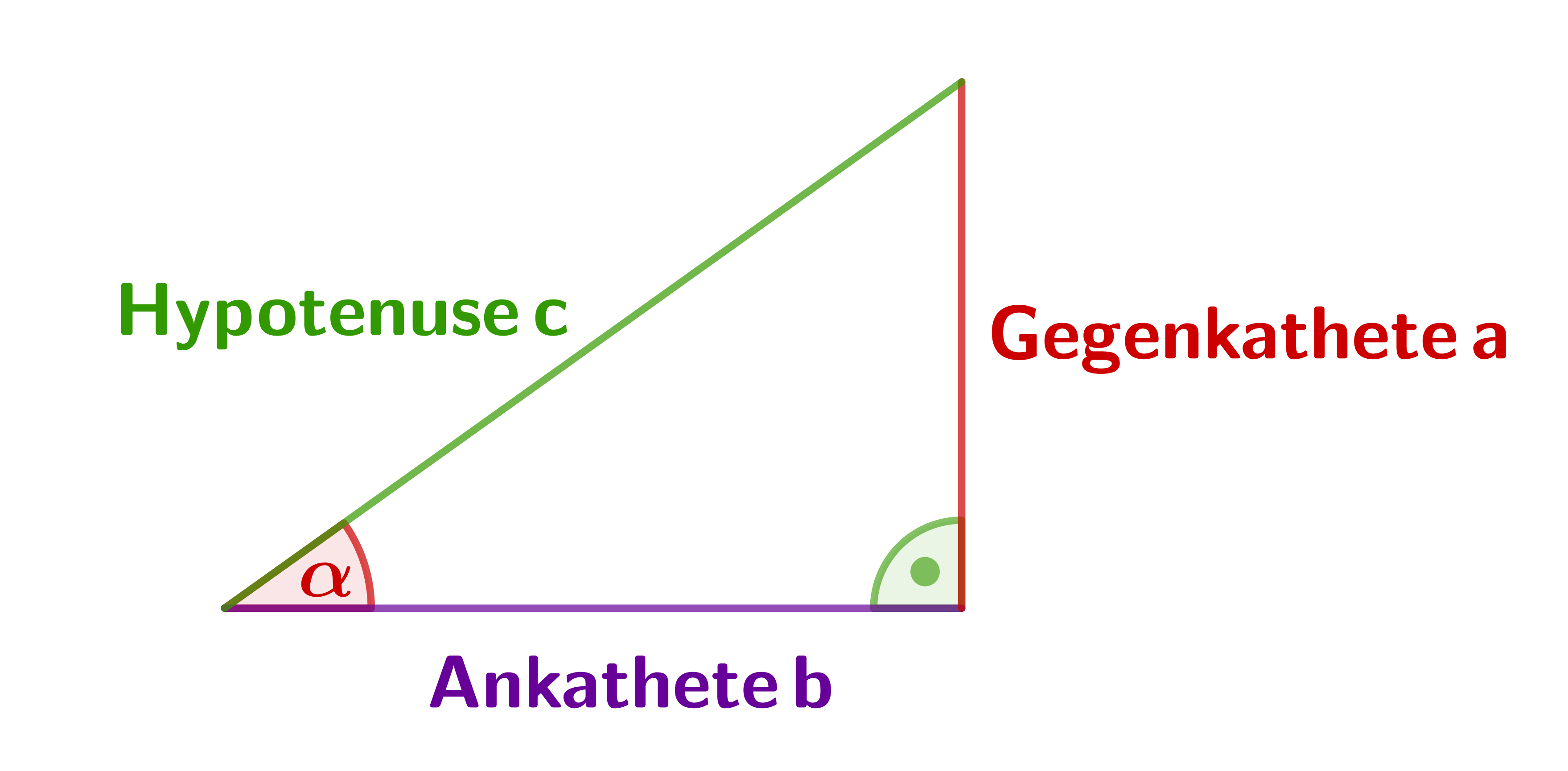
Er beschreibt das Verhältnis von Gegenkathete zu Hypotenuse. Der Sinus von \alpha (geschrieben \sin( \alpha)) ist die Gegenkathete von \alpha geteilt durch die Hypotenuse. Somit beschreibt \sin( \alpha) das Verhältnis der Längen von Gegenkathete und Hypotenuse.Der Sinussatz besagt, dass das der Sinuswerte zweier eines Dreiecks dem Verhältnis der diesen Winkeln Seiten entspricht.
Wann Sinus und wann Kosinussatz : Du kannst den Kosinussatz nur verwenden, wenn du zwei Seiten und den Winkel dazwischen kennst. Ist der Winkel gegenüber einer Seite bekannt, kann dir stattdessen oft der Sinussatz weiterhelfen.
Wie ist der Kosinussatz
Der Kosinussatz für ein Dreieck ABC lautet a2=b2+c2-2bc·cos(α).
Was ist die Cosinus Formel : sin(α)= Gegenkathete / Hypotenuse. cos(α)= Ankathete / Hypotenuse. tan(α)= Gegenkathete / Ankathete.
Der Sinus ist eine wichtige trigonometrische Funktion, mit welcher du zum einen Winkel in einem rechtwinkligen Dreieck berechnen kannst und zum anderen ist er sehr nützlich, um periodische Vorgänge in der Physik zu beschreiben, wie zum Beispiel Wellen.
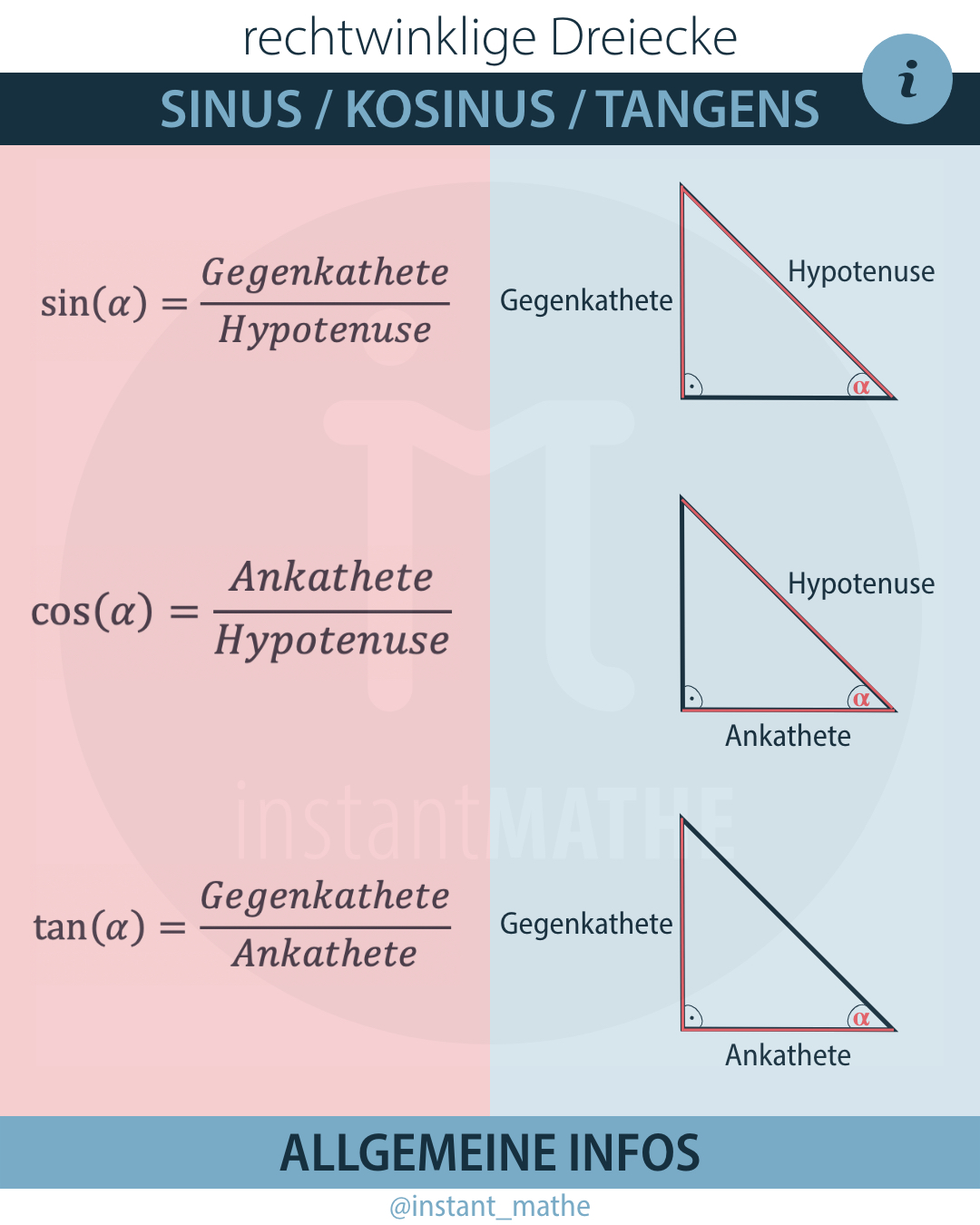
sin(α)= Gegenkathete / Hypotenuse. cos(α)= Ankathete / Hypotenuse.
Was sagt der Kosinussatz aus
Der Kosinussatz besagt, dass das Quadrat einer Seite gleich der Summe der Quadrate der anderen Seiten ist. Diese ist gleich dem doppelten Produkt dieser Seiten und des von ihnen eingeschlossenen Winkels.Also zum Beispiel die Seiten b und c und den Winkel α in diesem Dreieck: Die Seite a ist durch b, c und α eindeutig bestimmt! Der Kosinussatz dient nun dazu, die Länge der Seite a rechnerisch zu bestimmen. Das kommt in der "Wirklichkeit" sehr häufig vor, z.B. bei Höhen- und Entfernungsbestimmungen.sin cos tan Tabelle
| Winkel α im Gradmaß | cos(α) gerundet |
|---|---|
| 30° (-330°) | 0,8660 |
| 45° (-315°) | 0,7071 |
| 60° (-300°) | 0,5000 |
| 75° (-285°) | 0,2588 |

Der genau Wert von cos(90°) cos ( 90 ° ) ist 0 .
Wie rechnet man den Sinus aus : sin(α)= Gegenkathete / Hypotenuse. cos(α)= Ankathete / Hypotenuse. tan(α)= Gegenkathete / Ankathete.
Wann rechnet man mit Sinus : Sinussatz. Den Sinussatz kannst du benutzen, um fehlende Stücke eines Dreiecks zu berechnen. Zum Beispiel, wenn zwei Seitenlängen und ein gegenüber liegender Winkel oder eine Seitenlänge und zwei Winkel gegeben sind. Das Dreieck muss dabei nicht rechtwinklig sein!
Was ist der Sinus von 45
sin cos tan Tabelle
| Winkel α im Gradmaß | sin(α) gerundet |
|---|---|
| 45° (-315°) | 0,7071 |
| 60° (-300°) | 0,8660 |
| 75° (-285°) | 0,9659 |
| 90° (-270°) | 1,0000 |
Nach der Definition ist der Sinus von 30 Grad gleich ½, und der Kosinus von 30 Grad ist √ 3/2.Der Kosinussatz ist einer der fundamentalen Lehrsätze der Geometrie und hier dem Gebiet der Trigonometrie zugehörig. Er ist eng verwandt mit dem Satz des Pythagoras. Für ebene Dreiecke ist der Kosinussatz sehr einfach zu formulieren, für sphärische benötigt er sechs Winkelfunktionen.
In welchen Dreiecken gilt der Kosinussatz : Der Satz des Pythagoras als Spezialfall des Kosinussatzes
Für γ = 9 0 ∘ \gamma=90^\circ γ=90∘ erhält man ein rechtwinkliges Dreieck und es gilt ( 9 0 ∘ ) = 0 \cos(90^\circ)=0 cos(90∘)=0. Damit ist der Satz des Pythagoras c 2 = a 2 + b 2 c^2=a^2+b^2 c2=a2+b2 ein Spezialfall des Kosinussatzes.