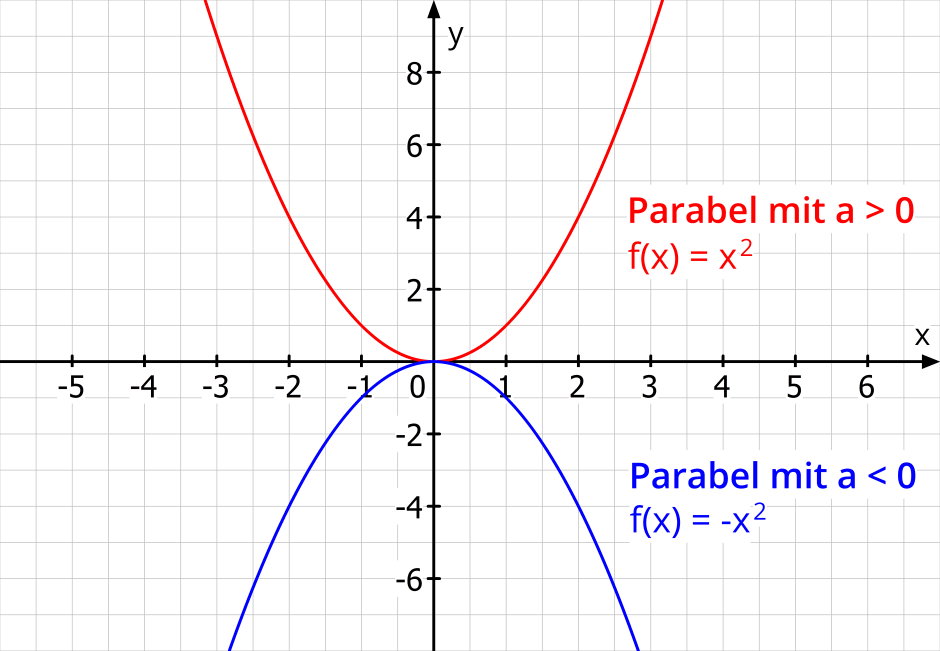
Der Graph einer quadratischen Funktion ist eine Parabel. über der Erdoberfläche befinden. beschreibt eine spezielle quadratische Funktion. ( a x 2 nennt man das quadratische Glied, bx das lineare Glied und c das absolute Glied der Funktionsgleichung).Was ist c in einer quadratischen Funktion Der Parameter a hat Auswirkungen auf die Form des Graphen. c ist das absolute Glied und gibt den y-Achsenabschnittspunkt an. Und b gibt an, wie steil der Graph am Punkt c ist.Die Gleichung y=ax2+bx+cheißt Parabelgleichung. Alle Punkte x | y , deren Koordinaten x und y diese Gleichung erfüllen, liegen somit auf der Parabel.
Für was steht B in einer Parabel : Parameter b: Verschiebung. Der Parameter b verschiebt die komplette Parabel sowohl in x- als auch in y-Richtung.
Was ist C bei quadratischen Funktion
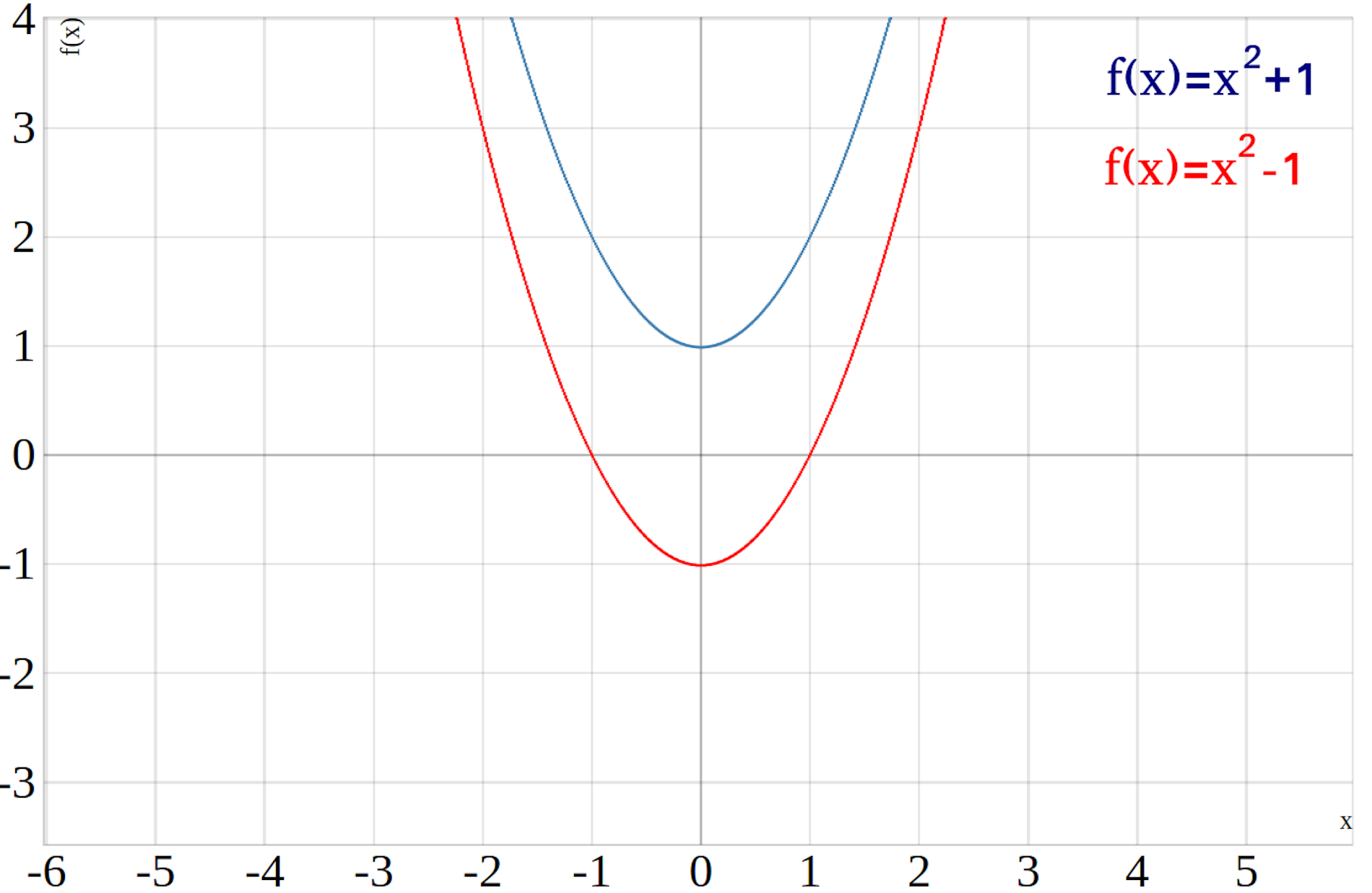
Das absolute Glied c verschiebt den Scheitelpunkt der Parabel entlang der y-Achse, also nach oben oder unten.
Was macht Parameter C : Parameter c verschiebt den Graphen in y-Richtung. Ist c>0 , dann verschiebt sich der Graph nach oben. Ist c=0 , genau dann verläuft der Graph durch den Ursprung. Ist c<0 , dann verschiebt sich der Graph nach unten.
Das absolute Glied c verschiebt den Scheitelpunkt der Parabel entlang der y-Achse, also nach oben oder unten.
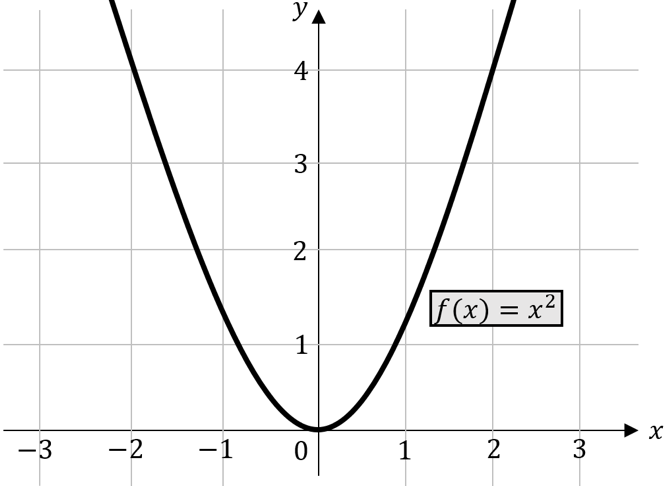
Parameter c verschiebt den Graphen in y-Richtung. Ist c>0 , dann verschiebt sich der Graph nach oben. Ist c=0 , genau dann verläuft der Graph durch den Ursprung.
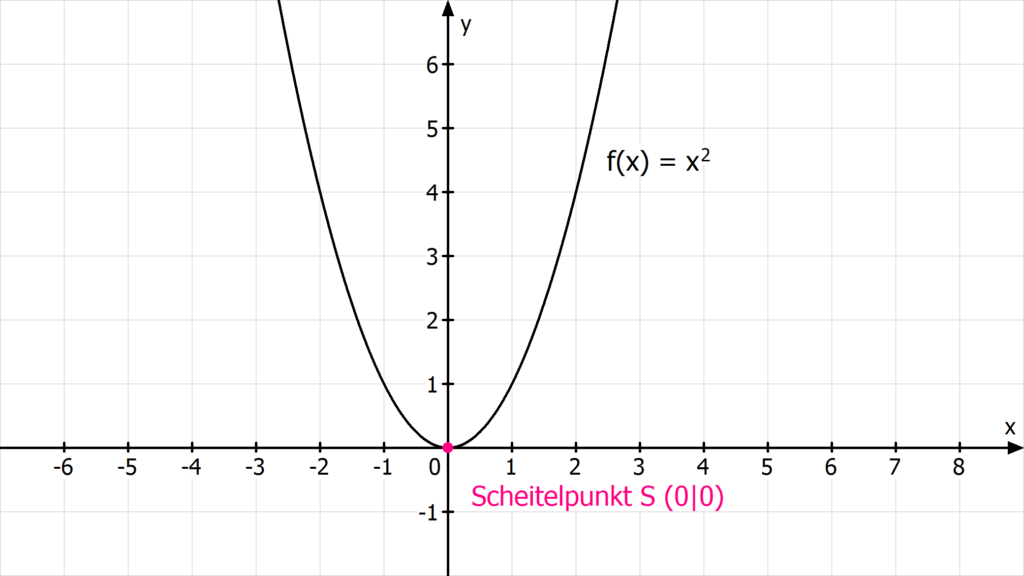
Was sagt die Scheitelpunktform aus
Der Scheitelpunkt ist der höchste bzw. tiefste Punkt einer Parabel. Du kannst den Scheitelpunkt aus der Scheitelpunktform f(x) = a(x-d)²+e ablesen: S (d | e).tiefste Punkt einer Parabel. Du kannst den Scheitelpunkt aus der Scheitelpunktform f(x) = a(x-d)²+e ablesen: S (d | e). Den Scheitelpunkt kannst du auch mit Hilfe der quadratischen Ergänzung , den binomischen Formeln oder der ersten Ableitung finden.Normalform: f(x)=ax2+bx+c. Scheitelpunktform: f(x)=a(x−d)2+e, dabei ist der Punkt S(d|e) der Scheitelpunkt der Parabel.
Bei einer gestreckten oder gestauchten Parabel f(x) = ax2 kannst du den Streckfaktor ganz einfach ablesen: er ist die Zahl a vor dem x2. Dieser Streckfaktor a bestimmt die Form der Parabel . Außerdem kannst du ablesen, ob die Parabel nach oben oder nach unten geöffnet ist: a positiv → nach oben geöffnet.
Was sagt der Scheitelpunkt aus : Der Scheitelpunkt S beschreibt entweder den höchsten (Sg) oder den niedrigsten Punkt (Sf) einer Parabel. Ist die Parabel nach oben geöffnet, ist der Scheitelpunkt ein Tiefpunkt, also der niedrigste Punkt. Ist die Parabel nach unten geöffnet, ist der Scheitelpunkt ein Hochpunkt, also der höchste Punkt.
Wie finde ich den Scheitelpunkt heraus : Demnach liegt der Scheitelpunkt genau in der Mitte zwischen den beiden Nullstellen. Die y-Koordinate e des Scheitelpunktes S berechnest Du, indem Du die x-Koordinate d in die Funktion f ( x ) = 2 3 · ( x + 1 ) · ( x – 3 ) einsetzt.
Was bedeutet C in der Normalform
Wir hatten uns die Allgemeinform einer quadratischen Funktion angeschaut, sie lautet: f(x) = a·x2 + b·x + c , wobei a , b und c reelle Zahlen sind und x die Variable.
Der Scheitelpunkt einer quadratischen Funktion ist immer der höchste oder niedrigste Punkt der Parabel! Spricht man von extremen Werten, ist der Scheitelpunkt einer nach unten geöffneten Parabel der maximale Termwert der Funktion.Allgemeiner bezeichnet man in der Differentialgeometrie einen Punkt auf einer regulären Kurve als Scheitel oder Scheitelpunkt, wenn die Krümmung dort ein lokales Extremum (also ein lokales Maximum oder Minimum) besitzt.
Wie lautet die Scheitelpunkt : tiefste Punkt einer Parabel. Du kannst den Scheitelpunkt aus der Scheitelpunktform f(x) = a(x-d)²+e ablesen: S (d | e). Den Scheitelpunkt kannst du auch mit Hilfe der quadratischen Ergänzung , den binomischen Formeln oder der ersten Ableitung finden.