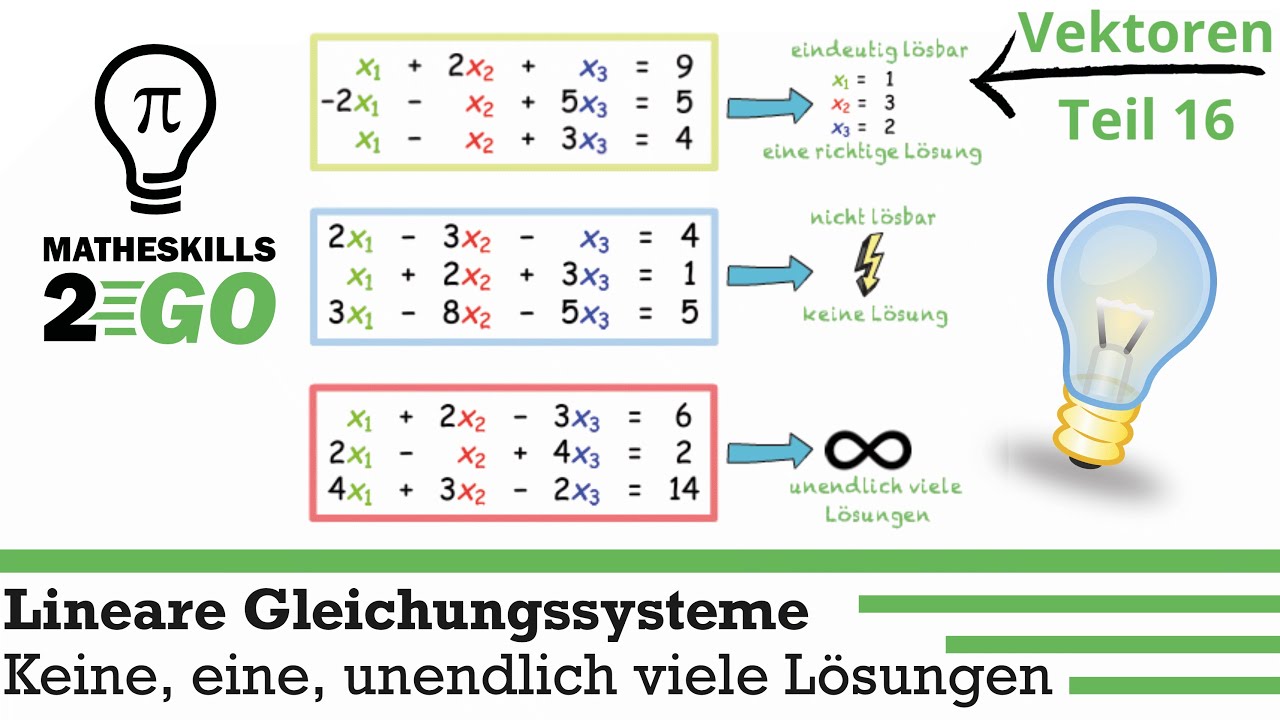
Ein lineares Gleichungssystem hat keine Lösung, wenn die Graphen parallel sind. Ein Koordinatensystem. Die x- und die y-Achse sind jeweils mit Einhalb skaliert. Der Graph einer Geraden geht durch die Punkte Null, Ein-Einhalb und Drei, Zwei.Damit ein LGS eindeutig lösbar ist, ist es wichtig, dass es genau so viele voneinander linear unabhängige Gleichungen gibt, wie es Unbekannte gibt. Zwei Gleichungen sind dabei linear abhängig , wenn man eine Gleichung so mit einer reellen Zahl multiplizieren kann, sodass dabei die zweite Gleichung entsteht.Ist der Rang der Koeffizientenmatrix kleiner als der Rang der erweiterten Koeffizientenmatrix, dann besitzt das Gleichungssystem keine Lösung.
Wann gibt es bei LGS eine Lösung : Ist der Rang der Koeffizientenmatrix gleich dem Rang der erweiterten Koeffizientenmatrix und auch gleich der Anzahl der Unbekannten, so besitzt das Gleichungssystem genau eine Lösung.
Was ist keine Lösung
· keine Lösung (parat) haben · (es ist) keine Lösung in Sicht (für) · (sich) keinen Rat wissen · mit seiner Weisheit am Ende sein · (sich) nicht mehr zu helfen wissen · (auch) nicht (mehr) weiterwissen · nicht wissen, was man machen soll · nicht wissen, was zu tun ist · passen müssen · (sich) die Haare raufen (ugs., …
Wie erkennt man, ob ein Gleichungssystem unendlich viele Lösungen hat : Wenn die beiden Linien den gleichen y-Achsenabschnitt und die gleiche Steigung haben, liegen sie tatsächlich auf derselben exakten Linie . Mit anderen Worten: Wenn die beiden Geraden dieselbe Gerade sind, sollte das System unendlich viele Lösungen haben. Das heißt, wenn das Gleichungssystem unendlich viele Lösungen hat, dann wird das System als konsistent bezeichnet.
Entsteht bei einem Gleichungssystem eine Nullzeile, so hat das LGS unendlich viele Lösungen. Man darf eine Variable als Parameter wählen und muss die Verbleibenden in Abhängigkeit dieses Parameters ausdrücken.
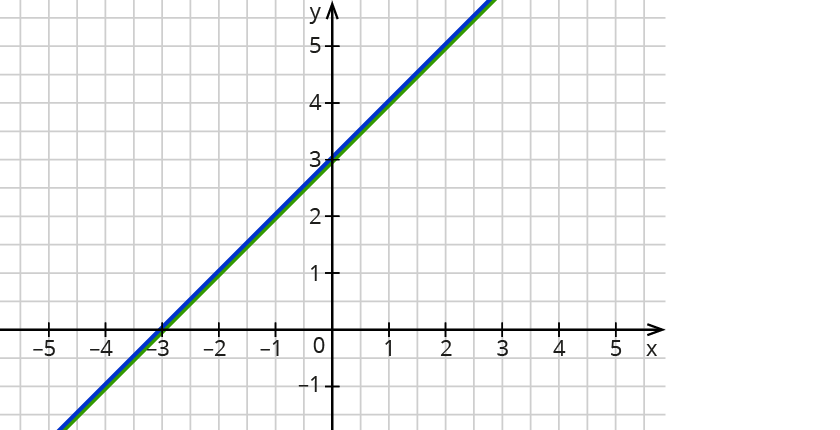
Wenn ein LGS unendlich viele Lösungen hat, erhältst du am Ende deiner Berechnung eine wahre Aussage. Dies kann zum Beispiel 4=4 sein.
Woher wissen Sie, ob eine Gleichung eine Lösung, keine Lösung oder unendlich viele Lösungen hat
Wenn wir die Gleichung lösen können und so etwas wie x=b erhalten, wobei b eine bestimmte Zahl ist, dann haben wir eine Lösung. Wenn wir am Ende eine Aussage erhalten, die immer falsch ist, etwa 3=5, dann gibt es keine Lösung . Wenn wir am Ende zu einer Aussage kommen, die immer wahr ist, wie 5=5, dann gibt es unendlich viele Lösungen. Erstellt von Sal Khan.Entsteht bei einem Gleichungssystem eine Nullzeile, so hat das LGS unendlich viele Lösungen. Man darf eine Variable als Parameter wählen und muss die Verbleibenden in Abhängigkeit dieses Parameters ausdrücken. Beispielaufgabe: x1−2×2+3×3=4.Ein homogenes lineares Gleichungssystem ist stets lösbar. Es besitzt immer den Nullvektor als Lösung (trivialen Lösung). Dieser ist genau dann die einzige Lösung, wenn der Rang der Koeffizientenmatrix gleich der Anzahl der Variablen ist.
Als Lösung bezeichnet man ein molekulardisperses, homogenes Gemisch, das aus einem oder mehreren gelösten Stoffen (Solvate) und einem Lösungsmittel (Solvens) besteht. Die gelösten Stoffe sind als Ionen oder kleine Molekülgruppen gleichmäßig im Lösungsmittel verteilt.
Wenn ein lineares Gleichungssystem keine Lösung hat : A system of linear equations that has no solution is called an inconsistent pair of linear equations. When we consider a system of linear equations, we can compare the coefficients of the equations and find whether it is a system of equations with no solution. We can determine the same from a graph also.
Welches Gleichungssystem hat genau eine Lösung : A consistent linear system of equations will have exactly one solution if and only if there is a leading 1 for each variable in the system. If a consistent linear system of equations has a free variable, it has infinite solutions.
Wie erkennt man, ob eine Gleichung unendlich viele Lösungen hat
Wenn wir am Ende auf beiden Seiten des Gleichheitszeichens den gleichen Term erhalten , etwa 4 = 4 oder 4x = 4x, dann haben wir unendlich viele Lösungen. Wenn wir am Ende auf beiden Seiten des Gleichheitszeichens unterschiedliche Zahlen haben, wie in 4 = 5, dann haben wir keine Lösungen.
Es sind mehr Variablen als Gleichungen gegeben, daher hat auch dieses System unendlich viele Lösungen.Ein homogenes Gleichungssystem Ax = 0 ist immer lösbar, d.h. hat immer eine Lösung, nämlich die triviale Lösung x =0. Ein inhomogenes Gleichungssystem Ax = b braucht hingegen nicht immer lösbar zu sein, wie man am Beispiel x1 + x2 = 1 , x1 + x2 = 2 sieht.
Hat ein lineares Gleichungssystem mehr Gleichungen als Variablen so hat es keine Lösung : Ja! Wenn die lineare Gleichung durch Äquivalenzumformungen zu einer allgemeingültigen Aussage geführt werden kann, hat die lineare Gleichung unendlich viele Lösungen. Ein Beispiel für eine lineare Gleichung mit unendlich vielen Lösungen ist: x = x x=x x=x .
