Mit dem Sinussatz berechnest Du fehlende Seitenlängen oder Winkel in einem beliebigen Dreieck, solange Du nur „Seiten-Winkel-Paar“ und eine weitere Größe kennst.Sinussatz. Der Sinussatz gibt eine Beziehung zwischen den Winkeln eines allgemeinen Dreiecks und den gegenüberliegenden Seiten an. Das bedeutet: Wenn du in einem allgemeinen Dreieck von je zwei Winkeln und den entsprechend gegenüberliegenden Seiten drei Größen kennst, kannst die fehlende vierte Größe berechnen.Mit dem Sinussatz kannst du Seiten und Winkel in jedem beliebigen Dreieck berechnen. Wenn du eine Seite und den gegenüberliegenden Winkel kennst, kannst du von einer anderen Größe (Seite oder Winkel) die gegenüberliegende Größe ausrechnen.

Wann nimmt man Sinus und wann Cosinus : Der Sinus eines Winkels ist das Verhältnis der Länge der Gegenkathete (Kathete, die dem Winkel gegenüberliegt) zur Länge der Hypotenuse (Seite gegenüber dem rechten Winkel). Der Kosinus ist das Verhältnis der Länge der Ankathete (das ist jene Kathete, die einen Schenkel des Winkels bildet) zur Länge der Hypotenuse.
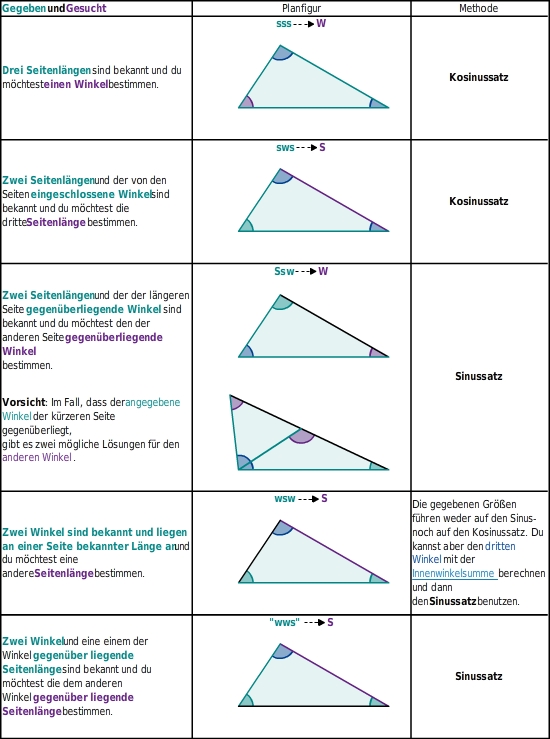
Wann ist der Kosinussatz anwendbar
Den Kosinussatz kannst Du in einem beliebigen Dreieck anwenden, wenn Du eine Seite berechnen möchtest und die zwei anderen Seiten, sowie der davon eingeschlossene Winkel gegeben sind. Außerdem kannst Du ihn anwenden, wenn in einem Dreieck alle Seiten gegeben sind und Du einen Winkel berechnen möchtest.
Was kann man mit Sinus berechnen : sin(α)= Gegenkathete / Hypotenuse. cos(α)= Ankathete / Hypotenuse. tan(α)= Gegenkathete / Ankathete.
Der Sinus ist nur im rechtwinkligen Dreieck definiert als Gegenkathete geteilt durch Hypotenuse. (Ausführliche Informationen und Übungsmaterial zum Sinus im rechtwinkligen Dreieck findest du auf der Seite LEARNZEPT.de.) Der Sinussatz hingegen gilt in einem beliebigen Dreieck.

Mit dem Sinus kann man entweder die Länge der Hypotenuse oder die Länge der Gegenkathete oder die Größe des Winkels berechnen, je nachdem, welche der drei Größen gesucht ist. Die jeweils anderen beiden Größen müssen gegeben sein.
Für welche Winkel gilt sin cos
Spiegelst du den Punkt P(x|y) an der x-Achse, dann erhälst du den Punkt P' mit den Koordinaten (x|-y). Liegt der zum Punkt P gehörige Winkel α zwischen 0° und 360°, dann ist der zum Punkt P' gehörige Winkel 360° – α. Wegen x=cos(α) und y=sin(α) gilt dann: cos(360°-α)=x und sin(360°-α)=-y.sin²(α) + cos²(α) = 1
Mit Hilfe dieser Beziehung kannst du ohne Taschenrechner zu jedem Winkel den Sinus aus dem Kosinus oder den Kosinus aus dem Sinus bestimmen. Wenn sin(α)=0.6 , dann cos(α)=0.8 .Kosinussatz – Herleitung und Beweis
Um den Kosinussatz zu beweisen, kannst Du als Grundlage den Satz des Pythagoras verwenden. Er gilt aber nur in rechtwinkligen Dreiecken.
Der Satz des Pythagoras als Spezialfall des Kosinussatzes
Für γ = 9 0 ∘ \gamma=90^\circ γ=90∘ erhält man ein rechtwinkliges Dreieck und es gilt ( 9 0 ∘ ) = 0 \cos(90^\circ)=0 cos(90∘)=0. Damit ist der Satz des Pythagoras c 2 = a 2 + b 2 c^2=a^2+b^2 c2=a2+b2 ein Spezialfall des Kosinussatzes.
Was sagt der Sinus aus : Der Sinus ist eine wichtige trigonometrische Funktion, mit welcher du zum einen Winkel in einem rechtwinkligen Dreieck berechnen kannst und zum anderen ist er sehr nützlich, um periodische Vorgänge in der Physik zu beschreiben, wie zum Beispiel Wellen.
Für was braucht man Sinus Kosinus und Tangens : Die drei trigonometrischen Funktionen Sinus, Kosinus und Tangens können mithilfe der Katheten und der Hypotenuse beschrieben werden. Mit diesen Formeln kannst Du in der Anwendung einige Seitenlängen und Winkel bei rechtwinkligen Dreiecken berechnen, auch wenn sie nicht alle gegeben sind.
Was ist die Formel für den Kathetensatz
Der Kathetensatz besagt, dass gilt: a² = p · c. b² = q · c.
sin cos tan Tabelle
| Winkel α im Gradmaß | sin(α) gerundet |
|---|---|
| 180° (-180°) | 0,0000 |
| 195° (-165°) | -0,2588 |
| 210° (-150°) | -0,5000 |
| 225° (-135°) | -0,7071 |
Der genau Wert von sin(90°) sin ( 90 ° ) ist 1 .
Wie groß ist der Sinus von 45 Grad : sin cos tan Tabelle
| Winkel α im Gradmaß | sin(α) gerundet |
|---|---|
| 45° (-315°) | 0,7071 |
| 60° (-300°) | 0,8660 |
| 75° (-285°) | 0,9659 |
| 90° (-270°) | 1,0000 |

