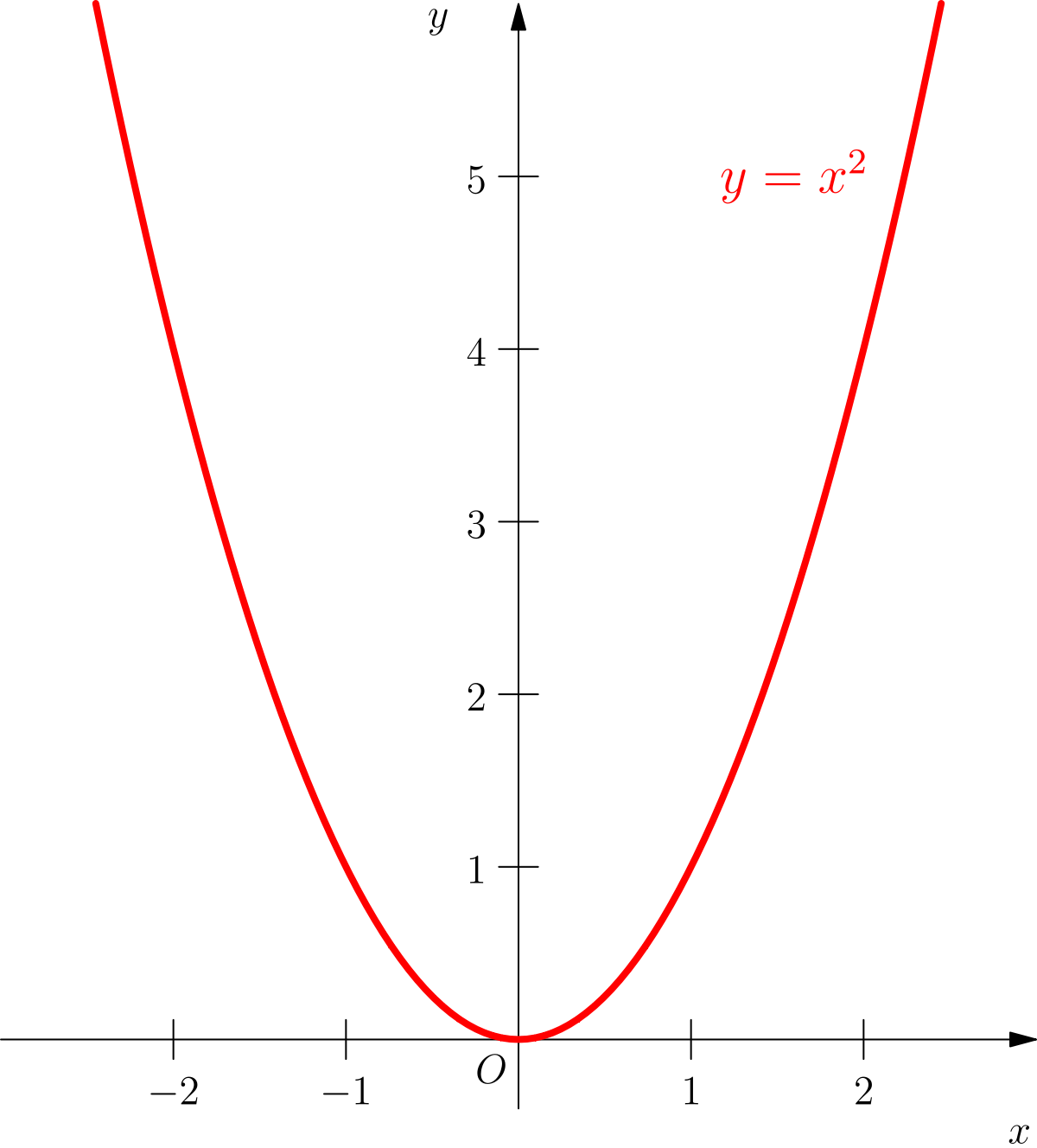
Die Normalparabel im Überblick
Eigenschaften der Normalparabel: Der Graph ist symmetrisch zur y-Achse. Der Graph geht nicht unter die x-Achse. Der Graph hat einen Tiefpunkt bei (0|0).Form: y = a(x−d) 2
Wenn a≠1 handelt es sich nicht um eine Normalparabel, sondern um eine gestreckte oder gestauchte Parabel. Für a>0 ist die Parabel nach oben geöffnet, für a<0 ist der Graph an der x-Achse gespiegelt, also die Parabel nach unten geöffnet.Eine Parabel ist eine kurze und lehrhafte Erzählung und gehört damit zu den epischen Kurzformen. Die Parabel besteht aus zwei Ebenen: Sie erzählt eine Geschichte im Vordergrund (Bildebene), aus der die Leser*innen die eigentliche Bedeutung auf der Metaebene (Sachebene) interpretieren sollen.
Wann ist die Normalparabel enger : Quadratische Funktion. Form: y=ax2
Diese Parabeln haben, wie die Normalparabel auch, den Scheitelpunkt S(0∣0) und sind ebenfalls symmetrisch zur y-Achse. Es gilt: Ist |a|>1, also a>1 oder a<−1, dann ist die Parabel enger als die Normalparabel (gestreckt, in der Skizze unten rot).
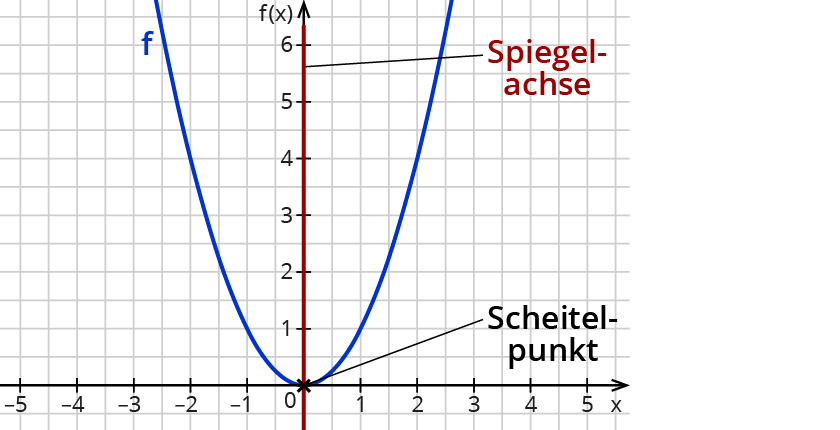
Was macht eine Normalparabel aus
Hochpunkt einer solchen bogenförmigen Parabel bezeichnet man als Scheitelpunkt. Die allgemeine Funktionsgleichung einer jeden Parabel lautet f ( x ) = a x 2 + b x + c Die einfachste Parabel mit der Funktionsgleichung f ( x ) = x 2 wird als Normalparabel bezeichnet.
Wie sieht ein Normalparabel aus : Die Gleichung y=ax2+bx+cheißt Parabelgleichung. Alle Punkte x | y , deren Koordinaten x und y diese Gleichung erfüllen, liegen somit auf der Parabel. Die einfachste quadratische Funktion hat die Gleichung y=f(x)=x2. Ihr Graph ist die Normalparabel.
Parabeln haben ein typisches bogenförmiges Aussehen und können nach oben oder nach unten geöffnet sein. Ihr eindeutig bestimmter tiefster bzw. höchster Punkt heißt Scheitelpunkt. Eine Parabel heißt Normalparabel, wenn ihre Funktionsgleichung f ( x ) = x 2 ~f(x)=x^2 f(x)=x2 lautet.
Stauchen und Strecken von Parabeln: 6 Fakten
Wenn a größer als 1 oder kleiner als -1 ist, dann ist die Funktion gestreckt. Wenn a zwischen 1 und -1 liegt, dann ist die Funktion gestaucht. Ist a=1 oder a=-1, dann ist der Graph von f eine Normalparabel oder eine umgekehrte Normalparabel.
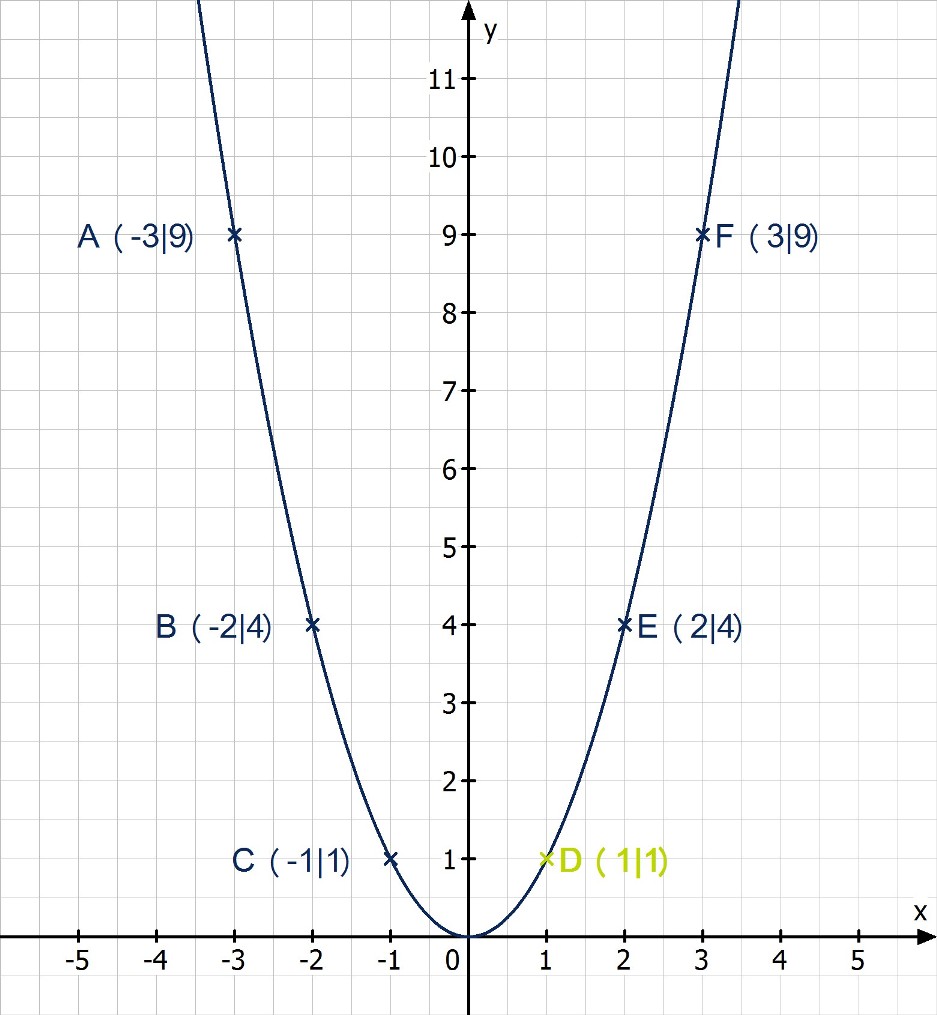
Was sind die Eigenschaften der Normalparabel
Der Graph der quadratischen Funktion y=x² heißt Normalparabel mit dem Scheitel S ( 0 | 0 ). Eigenschaften der Funktion / des Graphen: Die Funktion y=x² ordnet jedem x-Wert seine Quadratzahl x² zu. Damit gilt: der y-Wert einer Zahl x und der y-Wert ihrer Gegenzahl -x sind immer gleich.Parabeln haben ein typisches bogenförmiges Aussehen und können nach oben oder nach unten geöffnet sein. Ihr eindeutig bestimmter tiefster bzw. höchster Punkt heißt Scheitelpunkt. Eine Parabel heißt Normalparabel, wenn ihre Funktionsgleichung f ( x ) = x 2 ~f(x)=x^2 f(x)=x2 lautet.
